如图,在菱形ABCD中,∠A=30°,取大于1/2 AB的长为半径,分别以点A,B为圆心作弧相交于两点,过此两点的直线交AD边于点E(作图痕迹如图所示),连接BE,BD,则∠EBD的度数为_________.
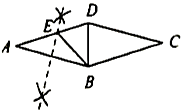
如图,在菱形ABCD中,∠A=30°,取大于1/2 AB的长为半径,分别以点A,B为圆心作弧相交于两点,过此两点的直线交AD边于点E(作图痕迹如图所示),连接BE,BD,则∠EBD的度数为_________.

45°
【解析】
∠ABC=180°-30°=150°
ABD=1/2∠ABC=75°
∵AE=EB
∴∠EAB=∠EBA
∴∠EBD=75°-30°=45°
如图,菱形ABCD中,点E是边CD的中点,EF垂直AB交AB的延长线于点F,若BF:CE=1:2,EF=√7,则菱形ABCD的边长是【 】
如图,在▱ABCD中,AC、BD交于点O,点E、F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;(2)若∠BAC=∠DAC.求证:四边形EBFD是菱形.
如图所示,在▱ABCD中,AB=5,AD=8,DE平分∠ADC,则BE=________.
如图,在平行四边形ABCD中,将△AB' C沿着AC所在的直线翻折得到△AB' C,B'C交AD于点E,连接B'D.若∠B=60°,∠ACB=45°,AC=.则B'D的长是【 】
如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F若DF=,则对角线BD的长为________(结果保留根号)
如图,将▱ABCD绕点A逆时针旋转到▱A'B'C'D'的位置,使点B'落在BC上,B'C'与CD交于点E,若AB=3,BC=4,BB'=1,则CE的长为______.
如图,在▱ABCD中,AD=5,AB=12,sinA=4/5.过点D作DE⊥AB,垂足为E,则sin∠BCE=________.
如图,在△ABC中,D,E分别为BC,AC上的点,将△CDE沿DE折叠,得到△FDE,连接BF,CF, ∠BFC=90°,若EF/AB,AB=4√3,EF=10,则AE的长为________.
如图,在矩形ABCD中,点E,F分别在BC,AD上,AF=EC只需添加一个条件即可证明四边形AECF是菱形,这个条件可以是__________(写出一个即可)。