如图,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.
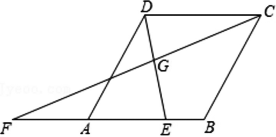
(1) 当点E运动到AB中点时,证明:四边形DFEC是平行四边形;
(2) 当CG=2时,求AE的长;
(3) 当点E从点A向右运动到点B时,求点G运动路径的长度.
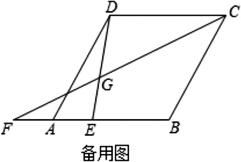
如图,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.


(1) 当点E运动到AB中点时,证明:四边形DFEC是平行四边形;
(2) 当CG=2时,求AE的长;
(3) 当点E从点A向右运动到点B时,求点G运动路径的长度.
(1) 连接DF,CE∵E为AB的中点,∴AE=AF=1/2 AB,∴EF=AB,∵四边形ABCD是菱形,∴EF//CD ,∵EF=AB=CD,∴四边形DFEC是平行四边形.(2) 作CH⊥BH,设AE=AF=m,如图所示,∵四边形ABCD是菱形,∴CD//EF,∴△CDG∼△EFG,∴CD/CG=EF/FG,∴FG=2m.在Rt△CBH中,由∠CBH=60°,BC=2,得CH=BC∙sin60°=√3,BH=BC∙cos60°=1.在Rt△CFH中,CF=2+2m,CH=√3,FH=3+m,由CH2+FH2=CF2得(√3)2+(3+m)2=(2+2m)2,整理得3m2+2m-8=0,解得m_1=4/3,m_2=-2(舍去),得AE=4/3.(3) G点的轨迹为线段AG,延长线段AG交CD于H,作HM⊥AB于M,作DN⊥AB于N.∵四边形ABCD是...
查看完整答案如图,将▱ABCD绕点A逆时针旋转到▱A'B'C'D'的位置,使点B'落在BC上,B'C'与CD交于点E,若AB=3,BC=4,BB'=1,则CE的长为______.
如图,在▱ABCD中,AD=5,AB=12,sinA=4/5.过点D作DE⊥AB,垂足为E,则sin∠BCE=________.
如图,四边形OABC是平行四边形,以点O为圆心,OC为半径的⊙O与AB相切于点B,与AO相交于点D,AO的延长线交⊙O于点E,连接EB交OC于点F,求∠C和∠E的度数.
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8,BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是【 】
如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是_______.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.
如图,在▱ABCD中AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是__________(结果保留π).
已知:如图,在四边形ABCD中,AB//CD,对角线AC、BD相交于点O,BO=DO.求证:四边形ABCD是平行四边形.
如图,在⊙O中,点A在弧BC上,∠BOC=100°,则∠BAC=__________.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,∠DCA=∠B. (1)求证:CD是⊙O的切线;(2)若DE⊥AB,垂足为E,DE交AC与点;求证:△DCF是等腰三角形.
一把直尺、60°的直角板和光盘如图摆放,A为60°角与直尺的交点,AB=3,则光盘的直径是【 】
如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4.(1)求∠POA的度数;(2)计算弦AB的长.