初中数学-中考试题(山西省 2020年平行四边形)

问答题（2020年山西省）

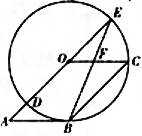
如图，四边形OABC是平行四边形，以点O为圆心，OC为半径的⊙O与AB相切于点B，与AO相交于点D，AO的延长线交⊙O于点E，连接EB交OC于点F，求∠C和∠E的度数．

答案解析

连接OB．∵AB与⊙O相切于点B，∴OB⊥AB．∴∠OBA=90°．∵四边形OABC是平行四边形，∴AB//OC∴∠BOC=∠OBA=90°∵OB=OC，∴∠C=∠OBC=1/2 (180°-∠BOC)=1/2×(...

查看完整答案

讨论

平行四边形

如图，在▱ABCD中，AD=5,AB=12,sinA=4/5.过点D作DE⊥AB，垂足为E，则sin∠BCE=________.

如图，在△ABC中，D,E分别为BC，AC上的点，将△CDE沿DE折叠，得到△FDE，连接BF,CF, ∠BFC=90°，若EF/AB，AB=4√3，EF=10,则AE的长为________.

如图，在菱形ABCD中，∠DAB=60°，AB=2，点E为边AB上一个动点，延长BA到点F，使AF=AE，且CF、DE相交于点G. (1) 当点E运动到AB中点时，证明：四边形DFEC是平行四边形；(2) 当CG=2时，求AE的长；(3) 当点E从点A向右运动到点B时，求点G运动路径的长度.

如图，在矩形ABCD中，点E，F分别在BC，AD上，AF=EC只需添加一个条件即可证明四边形AECF是菱形，这个条件可以是__________(写出一个即可)。

如图，在四边形ABCD中，∠ACB=∠CAD=90°，点E在BC上，AE//DC,EF⊥AB，垂足为F.(1)求证：四边形AECD是平行四边形；(2)若AE平分∠BAC,BE=5,cosB=4/5，求BF和AD的长.

如图，已知菱形ABCD的边长为2，∠DAB=60°，E为AB的中点，F为CE的中点，AF与DE相交于点G，则GF的长等于________.

阅读短文，解决问题.如果一个三角形和一个菱形满足条件：三角形的一个角与菱形的一个角重合，且菱形的这个角的对角顶点在三角形的这个角的对边上，则称这个菱形为该三角形的“亲密菱形”.如图(1)，菱形AEFD为△ABC的“亲密菱形”.如图(2)，在△ABC中，以点A为圆心，以任意长为半径作弧，交AB、AC于点M、N，再分别以M、N为圆心，以大于1/2 MN的长为半径作弧，两弧交点于P，作射线AP，交BC于点F,过点F作FD//AC，FE//AB.(1)求证：四边形AEFD是△ABC的“亲密菱形”；(2)当AB=6，AC=12，∠BAC=45°时，求菱形AEFD的面积.

已知菱形ABCD，E、F是动点，边长为4，BE=AF，∠BAD=120°，则下列结论正确的有几个【】。①△BEC≌△AFC；②△CFE为等边三角形；③∠AGE=∠AFC；④若AF=1，则GF/EG=1/3.

如图，将矩形ABCD沿直线EF折叠，使点C与点A重合，折痕交AD于点E，交BC于点F，连接AF、CE.(1)求证：四边形AFCE为菱形;(2)设AE=a，ED=b，DC=c.请写出一个a、b、c三者之间的数量关系式.

根据所标数据，下列一定为平行四边形的是【】

四边形

由沈康身教授所著，数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事：如图，三姐妹为了平分一块边长为1的祖传正方形地毯，先将地毯分割成七块，再拼成三个小正方形(阴影部分).则图中AB的长应是________.

探究：是否存在一个新矩形，使其周长和面积为原矩形的2倍、1/2倍、k倍。(1)若该矩形为正方形，是否存在一个正方形，使其周长和面积都为边长为2的正方形的2倍?________(填“存在”或“不存在”)。(2)继续探究，是否存在一个矩形，使其周长和面积都为长为3，宽为2的矩形的2倍?同学们有以下思路:①设新矩形长和宽为x,y，则依题意有x+y=10，xy=12，得x2-10x+12=0，再探究根的情况;根据此方法，请你探究是否存在一个矩形，使其周长和面积都为原矩形的1/2倍；②如图也可用反比例函数与一次函数证明l1:y=-x+10 ,l2:y=12/x.那么，a.是否存在一个新矩形为原矩形周长和面积的2倍?________.b.请探究是否有一新矩形周长和面积为原矩形的1/2，若存在，用图像表达:c.请直接写出当结论成立时k的取值范围:____________.

如图，O为正方形ABCD对角线AC的中点，ΔACE为等边三角形.若AB=2，则OE的长度为【】

如图，在正方形ABCD中，点E是边BC上的一点，点F在边CD的延长线上，且BE=DF，连接EF交边AD于点G.过点A作AN〦EF，垂足为点M，交边CD于点N.若BE=5，CN=8，则线段AN的长为________.

如图，正方形ABCD中，点E、F分别在边BC、CD上，AE=AF，∠EAF=30°，则∠AEB=______°；若△AEF的面积等于1，则AB的值是______.

如图1，矩形ABCD中，AB=6，AD=8，点P在边BC上，且不与点B、C重合，直线AP与DC的延长线交于点E.(1)当点P是BC的中点时，求证：△ABP≌△ECP；(2)将△APB沿直线AP折叠得到△APB'，点B'落在矩形ABCD的内部，延长PB'交直线AD于点F.①证明FA=FP，并求出在(1)条件下AF的值；②连接B'C，求△PCB'周长的最小值；③如图2，BB'交AE于点H，点G是AE的中点，当∠EAB'=2∠AEB'时，请判断AB与HG的数量关系，并说明理由.

如图，在等腰梯形ABCD中，已知AD//BC,AB=DC，AC与BD交于点O，延长BC到E，使得CE=AD，连接DE. (1)求证：BD=DE.(2)若AC⊥BD,AD=3,SABCD=16，求AB的长.

如图，已知四边形ABCD为等腰梯形，AD//BC,AB=CD,AD=√2,E为CD中点，连接AE，且AE=2√3,∠DAE=30°，作AF⊥AE交BC于F，则BF=【】

一个矩形周长为56 厘米.(1)当矩形面积为180平方厘米时，长宽分别为多少?(2)能围成面积为200平方厘米的矩形吗?请说明理由.

如图，在正方形ABCD中，BE=1，将BC沿CE翻折，使B点对应点刚好落在对角线AC上，将AD沿AF翻折，使D点对应点刚好落在对角线AC上，求EF=______.

几何图形

如图，PA与⊙O相切于A点，弦AB⊥OP，垂足为C，OP与⊙O相交于D点，已知OA=2，OP=4.(1)求∠POA的度数；(2)计算弦AB的长.

如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠A=40°，则∠C=________.

如图1(左)，将一个正六边形各边延长，构成一个正六角星形 AFBDCE，它的面积为1，取△ABC和△DEF各边中点，连接成正六角星形 A1F1B1D1C1E1，如图2(中)中阴影部分，取△A1B1C1和△D1E1F1各边中点，连接成正六角星形A2F2D2C2E2，如图3(右)中阴影部分，如此下去…，则正六角星形 A4F4B4D4C4E4的面积为________.

如图，在平面直角坐标系中，点P的坐标为(-4，0)，⊙P的半径为2，将⊙P沿x轴向右平移4个单位长度得⊙P1.(1)画出⊙P1，并直接判断⊙P与⊙P1的位置关系；(2)设⊙P1与x轴正半轴，y轴正半轴的交点分别为A、B.求劣弧AB与弦AB围成的图形的面积(结果保留π).

如图所示的几何体的主视图是【】

如图，A、B、C是⊙O上的三个点，∠ABC=25°，则∠AOC=________.

如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是【】

如图所示,是一个由若干个相同的小正方体组成的几何体的主视图(左)和俯视图(右),则能组成这个几何体的小正方体的个数最少是______个。

如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行______分钟可使渔船到达离灯塔距离最近的位置.

如图所示的物体是一个几何体，其主视图是【】