根据所标数据,下列一定为平行四边形的是【 】
A、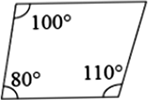
B、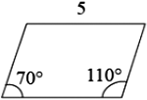
C、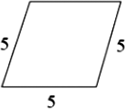
D、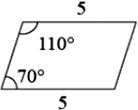
根据所标数据,下列一定为平行四边形的是【 】
A、
B、
C、
D、
D
【解析】
平行四边形对角相等,故A错误;
一组对边平行不能判断四边形是平行四边形,故B错误;
三边相等不能判断四边形是平行四边形,故C错误;
一组对边平行且相等的四边形是平行四边形,故D正确;
如图,在菱形ABCD中,对角线AC、BD相交于点O,H为BC中点,AC=6,BD=8.则线段OH的长为【 】
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8,BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是【 】
如图,在▱ABCD中AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是__________(结果保留π).
已知:如图,在四边形ABCD中,AB//CD,对角线AC、BD相交于点O,BO=DO.求证:四边形ABCD是平行四边形.
如图所示,在▱ABCD中,AB=5,AD=8,DE平分∠ADC,则BE=________.
如图,在平行四边形ABCD中,将△AB' C沿着AC所在的直线翻折得到△AB' C,B'C交AD于点E,连接B'D.若∠B=60°,∠ACB=45°,AC=.则B'D的长是【 】
如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F若DF=,则对角线BD的长为________(结果保留根号)