如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE.
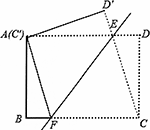
(1)求证:四边形AFCE为菱形;
(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE.

(1)求证:四边形AFCE为菱形;
(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.
(1)∵四边形ABCD是矩形,∴AD//BC,∴∠AEF=∠EFC,由折叠的性质,可得:∠AEF=∠CEF,AE=CE,AF=CF,∴∠EFC=∠CEF,∴CF=CE,∴AF=CF=CE=AE,∴四边形AFCE为菱形.(2)a、b、c三者之间的数量关...
查看完整答案如图,在矩形ABCD中,点E,F分别在BC,AD上,AF=EC只需添加一个条件即可证明四边形AECF是菱形,这个条件可以是__________(写出一个即可)。
如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE的中点,AF与DE相交于点G,则GF的长等于________.
如图,菱形ABCD中,点E是边CD的中点,EF垂直AB交AB的延长线于点F,若BF:CE=1:2,EF=√7,则菱形ABCD的边长是【 】
如图,在▱ABCD中,AC、BD交于点O,点E、F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;(2)若∠BAC=∠DAC.求证:四边形EBFD是菱形.
如图,四边形ACDF 是正方形,∠CEA和∠ABF 都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是______.
如图,在正方形ABCD中,BE=1,将BC沿CE翻折,使B点对应点刚好落在对角线AC上,将AD沿AF翻折,使D点对应点刚好落在对角线AC上,求EF=______.
如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积24cm2是的有盖的长方体铁盒.则剪去的正方形的边长为______cm.
如图,点O是正方形,ABCD的中心. (1)用直尺和圆规在正方形内部作一点E (异于点O),使得EB=EC; (保留作图痕迹,不写作法)(2)连接EB、EC、EO,求证:∠BEO=∠CEO.