如图,点O是正方形,ABCD的中心.
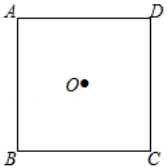
(1)用直尺和圆规在正方形内部作一点E (异于点O),使得EB=EC; (保留作图痕迹,不写作法)
(2)连接EB、EC、EO,求证:∠BEO=∠CEO.
如图,点O是正方形,ABCD的中心.

(1)用直尺和圆规在正方形内部作一点E (异于点O),使得EB=EC; (保留作图痕迹,不写作法)
(2)连接EB、EC、EO,求证:∠BEO=∠CEO.
(1)如图所示,点E即为所求.
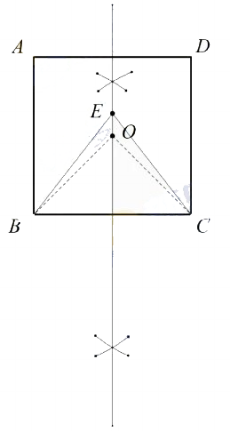
(2)连接OB、OC
由(1)得:EB=EC
∵O是正方形ABCD中心,
∴OB=OC,
∴在△EBO和△ECO中,

∴△EBO≅△ECO(SSS),
∴∠BEO=∠CEO.
如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是【 】
如图所示的几何体是由6个大小相同的小立方块搭成,它的俯视图是【 】
如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为【 】
下图是一个由5个相同的正方体组成的立体图形,它的主视图是【 】
如图①,用一个平面截长方体,得到如图②的几何体,它在我国古代数学名著《九章算术》中被称为“堑堵”.图②“堑堵”的俯视图是【 】
如图,AB是⊙O的切线,B为切点,OA与⊙O交于点C,以点A为圆心、以OC的长为半径 作(EF) ̂,分别交AB,AC于点E,F.若OC=2,AB=4,则图中阴影部分的面积为__________.