图①是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果。图②是一个菱形,将图②截去一个边长为原来一半的菱形得到图③,用图3镶嵌得到图④,将图④着色后再次镶嵌便得到图①,则图④中∠ABC的度数是________.
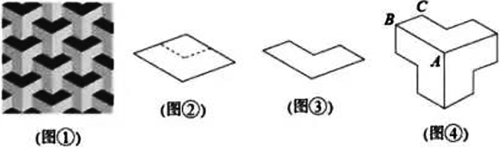
图①是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果。图②是一个菱形,将图②截去一个边长为原来一半的菱形得到图③,用图3镶嵌得到图④,将图④着色后再次镶嵌便得到图①,则图④中∠ABC的度数是________.

60°
【解析】
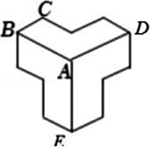
如图,∠BAD+∠BAE+∠DAE=360°,
又因为三个角相等,所以∠BAD=∠BAE=∠DAE=120°
BC//AD
∠ABC=180°-120°=60°.
如图所示,在▱ABCD中,AB=5,AD=8,DE平分∠ADC,则BE=________.
如图,在平行四边形ABCD中,将△AB' C沿着AC所在的直线翻折得到△AB' C,B'C交AD于点E,连接B'D.若∠B=60°,∠ACB=45°,AC=.则B'D的长是【 】
如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F若DF=,则对角线BD的长为________(结果保留根号)
如图,将▱ABCD绕点A逆时针旋转到▱A'B'C'D'的位置,使点B'落在BC上,B'C'与CD交于点E,若AB=3,BC=4,BB'=1,则CE的长为______.
如图,在▱ABCD中,AD=5,AB=12,sinA=4/5.过点D作DE⊥AB,垂足为E,则sin∠BCE=________.
如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE的中点,AF与DE相交于点G,则GF的长等于________.
如图,四边形OABC是平行四边形,以点O为圆心,OC为半径的⊙O与AB相切于点B,与AO相交于点D,AO的延长线交⊙O于点E,连接EB交OC于点F,求∠C和∠E的度数.
如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是【 】
一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若∠1=20°,则∠2的度数是【 】
如图,我国某海域有A,B两个港口,相距80海里,港口B在港口A的东北方向,点C处有一艘货船,该货船在港口A的北偏西30°方向,在港口B的北偏西75°方向,求货船与港口A之间的距离.(结果保留根号)
如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B=_______.
如图,已知∠1=70°,如果CD//BE,那么∠B的度数为【 】
如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是【 】
如图,直线a,b被直线c所截,A//b,∠1=60°.那么∠2=________°
如图,AB//CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.求证:∠DEF=∠F.
如图,直线a,b被c,d所截,且a//b,则下列结论中正确的是【 】
如图,直线m//n,△ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140° ,则∠2的度数是【 】
如图,在矩形ABCD中,若AB=3,AC=5,AF/FC=1/4,则AE的长为________.
如图,已知l1//l2//l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是【 】
如图,Rt△ABC是一块直角三角板,其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A,若DE//CB,则∠DAB的度数为【 】
如图,正六边形ABCDEF内接于⨀O.点M在(AB) ̂上则∠CME的度数为【 】
我国古代数学家祖冲之推算出π的近似值为355/113,它与π的误差小于0.0000003.将0.0000003用科学记数法可以表示为【 】