性质探究
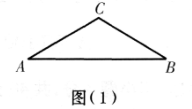
如图(1),在等腰三角形ABC中,∠ACB=120°,则底边AB与腰AC的长度之比为_________.
理解运用
(1)若顶角为120°的等腰三角形的周长为4+2√3,则它的面积为_________;
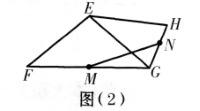
(2)如图(2),在四边形EFGH中,EF=EG=EH.在边FG,GH上分别取中点M,N,连接MN.若∠FGH=120°,EF=20,求线段MN的长.
类比拓展
顶角为2α的等腰三角形的底边与一腰的长度之比为__________(用含α的式子表示)
性质探究
如图(1),在等腰三角形ABC中,∠ACB=120°,则底边AB与腰AC的长度之比为_________.

理解运用
(1)若顶角为120°的等腰三角形的周长为4+2√3,则它的面积为_________;
(2)如图(2),在四边形EFGH中,EF=EG=EH.在边FG,GH上分别取中点M,N,连接MN.若∠FGH=120°,EF=20,求线段MN的长.

类比拓展
顶角为2α的等腰三角形的底边与一腰的长度之比为__________(用含α的式子表示)
性质探究:1(或)解法提示:过点C作CD⊥AB于点D,∵ΔABC是等腰三角形,∠ACB=120°∴∠CAB=30°,AD=DB,∴AB=2AD=2×AC×cos30º=AC∴AB:AC=:1理解运用(1)(2)解:∵∠FGH=120°,EF=EG=EH∴∠EFG+∠EHG=∠FGE+∠HGE=∠FGH=120°又∵∠FEH...
查看完整答案