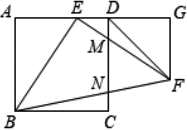
如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF,请完成下列问题:
(1) ∠FDG=______°;
(2)若DE=1,DF=2√2,则MN=________.
如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF,请完成下列问题:

(1) ∠FDG=______°;
(2)若DE=1,DF=2√2,则MN=________.
(1)45;(2)26/15(1)∵四边形ABCD是正方形,∴∠A=90°,AB=AD,∴∠ABE+∠AEB=90°,∵FG⊥AG,∴∠G=∠A=90°,∴∠AEB+∠FEG=90°,∴∠FEG=∠EBA,在△ABE和△GEF中,∠A=∠G,∠ABE=∠GEF,BE=EF,∴△ABE≅△GEF(AAS),∴AE=FG,AB=GE,又∵AB=AD,∴AD=GE,∴AE=DG=FG,∴∠FDG=∠DFG=45°.(2)如图,作FH⊥CD于H,∴∠FHD=90°∴四边形DGF...
查看完整答案泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的【 】
已知ΔABC的周长为16,点D,E,F分别为ΔABC三条边的中点,则ΔDEF的周长为【 】
如图,BC//DE,且BC<DE,AD=BC=4,AB+DE=10,则AE/AC的值为__________.
如图,在ΔABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D,若BC=4,则CD的长为_________.
如图,每个小正方形边长均为1,则图中的三角形(阴影部分)与下图中△ABC相似的是【 】
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为【 】
在Rt△ABC中,∠C=90°,AD平分∠CAB,BE平分∠ABC,AD,BE相交于点F,且AF=4,EF=√2,则AC=________.
如图,在正方形ABCD中,BE=1,将BC沿CE翻折,使B点对应点刚好落在对角线AC上,将AD沿AF翻折,使D点对应点刚好落在对角线AC上,求EF=______.
如图,四边形ACDF 是正方形,∠CEA和∠ABF 都是直角且点E,A,B三点共线,AB=4,则阴影部分的面积是______.
如图,点O是正方形,ABCD的中心. (1)用直尺和圆规在正方形内部作一点E (异于点O),使得EB=EC; (保留作图痕迹,不写作法)(2)连接EB、EC、EO,求证:∠BEO=∠CEO.
如图,O为正方形ABCD对角线AC的中点,ΔACE为等边三角形.若AB=2,则OE的长度为【 】
如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,∠EAF=30°,则∠AEB=______°;若△AEF的面积等于1,则AB的值是______.
如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是_______.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.
如图,在▱ABCD中AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是__________(结果保留π).
如图,将▱ABCD绕点A逆时针旋转到▱A'B'C'D'的位置,使点B'落在BC上,B'C'与CD交于点E,若AB=3,BC=4,BB'=1,则CE的长为______.
如图,在▱ABCD中,AD=5,AB=12,sinA=4/5.过点D作DE⊥AB,垂足为E,则sin∠BCE=________.