如图①,正方形ABCD中,AC,BD相交于点O,E是OD的中点.动点P从点E出发,沿着E→O→B→A的路径以每秒1个单位长度的速度运动到点A,在此过程中线段AP的长度y随着运动时间x的函数关系如图②所示,则AB的长为【 】

A、4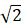
B、4
C、3
D、2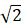
如图①,正方形ABCD中,AC,BD相交于点O,E是OD的中点.动点P从点E出发,沿着E→O→B→A的路径以每秒1个单位长度的速度运动到点A,在此过程中线段AP的长度y随着运动时间x的函数关系如图②所示,则AB的长为【 】

A、4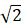
B、4
C、3
D、2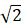
A