如图,从一块半径为1m 的圆形铁皮上剪出一个圆周角为120°的扇形ABC,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为_________m.
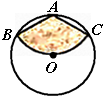
如图,从一块半径为1m 的圆形铁皮上剪出一个圆周角为120°的扇形ABC,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为_________m.

1/3
①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择【 】
平面内,将长分别为 1,5,1,1,d的线段,顺次首尾相接组成凸五边形(如图),则d可能是【 】
如图是钉板示意图,每相邻4个钉点是边长为1个单位长的小正方形顶点,钉点A,B的连线与钉点 C,D的连线交于点E,则(1)AB与CD是否垂直?______(填是”或否")(2)AE=______.
如图,Rt△ABC是一块直角三角板,其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A,若DE//CB,则∠DAB的度数为【 】
如图,扇形纸片AOB的半径为3,沿AB折叠扇形纸片,点O恰好落在(AB) ̂上的C处,图中阴影部分的面积为【 】
下图是由5个完全相同的小正方体摆成的几何体,则这个几何体的主视图是【 】
如图,直线m//n,△ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140° ,则∠2的度数是【 】
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是弧(AB) ̂的中点,点D在OB上,点E在OB 的延长线上,当正方形CDEF的边长为2√2时,阴影部分的面积为【 】
如图,AB是⊙O的切线,B为切点,OA与⊙O交于点C,以点A为圆心、以OC的长为半径 作(EF) ̂,分别交AB,AC于点E,F.若OC=2,AB=4,则图中阴影部分的面积为__________.
如图所示,若用半径为8,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是_________.