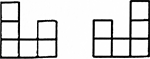
如图所示,是一个由若干个相同的小正方体组成的几何体的主视图(左)和俯视图(右),则能组成这个几何体的小正方体的个数最少是______个。
如图所示,在▱ABCD中,AB=5,AD=8,DE平分∠ADC,则BE=________.
如图所示,点P(3a,a)是反比例函数y=k/x(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为【 】
有四张质地相同的卡片,它们的背面相同,其中两张的正面印有“粽子”的图标,另外两张的正面印有“龙舟”的图案,现将它们背面朝上,洗均匀后排列在桌面,任意翻开两张,那么两张图案一样的概率是【 】
如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是【 】
观察下列算式,用你所发现的规律得出22015的末位数字是【 】21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…