关注蜜蜂引路，注册平台账号.
木门常常需要雕刻美丽的图案.
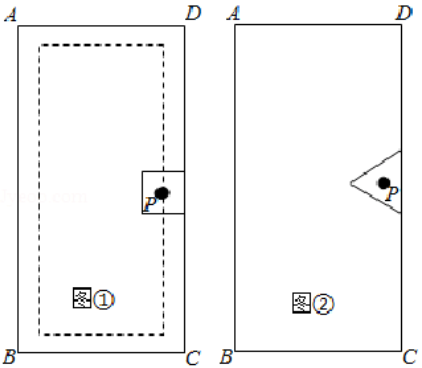
(1)图①为某矩形木门示意图，其中AB长为200厘米，AD长为100厘米，阴影部分是边长为30厘米的正方形雕刻模具，刻刀的位置在模具的中心点P处，在雕刻时始终保持模具的一边紧贴木门的一边，所刻图案如虚线所示，求图案的周长；
(2)如图②，对于(1)中的木门，当模具换成边长为30
厘米的等边三角形时，刻刀的位置仍在模具的中心点P处，雕刻时也始终保持模具的一边紧贴本门的一边，使模具进行滑动雕刻.但当模具的一个顶点与木门的一个顶点重合时，需将模具绕着重合点进行旋转雕刻，直到模具的另一边与木门的另一边重合.再滑动模具进行雕刻，如此雕刻一周，请在图②中画出雕刻所得图案的草阁，并求其周长.
(1)如图，过点P作PE⊥CD,垂足为E ∵P是边长为30cm的正方形模具的中心，∴PE=15cm,同理:A' B'与AB之间的距离为15cm,A'D'与AD之间的距离为15cm,B'C'与BC之间的距离为15cm,∴A'B'=C'D'=200-15-15=170cm,B'C'=A'D'=100-15-15=70cm,∴C_(四边形A'B' C' D')=(170+70)×2=480cm.答:图案的周长为480cm.(2)连接PE、PF、PG,过点P作PQ⊥CD，垂足为Q ∵P是边长为30cm的等边三角形模具的中心，∴PE=PG=PF,∠PG...
查看完整答案如图，菱形ABCD中，点E是边CD的中点，EF垂直AB交AB的延长线于点F，若BF:CE=1:2，EF=√7，则菱形ABCD的边长是【 】
如图，正方形ABCD中，点E、F分别在边BC、CD上，AE=AF，∠EAF=30°，则∠AEB=______°；若△AEF的面积等于1，则AB的值是______.
如图，在▱ABCD中，AC、BD交于点O，点E、F在AC上，AE=CF.(1)求证：四边形EBFD是平行四边形;(2)若∠BAC=∠DAC.求证：四边形EBFD是菱形.
如图，已知四边形ABCD为等腰梯形，AD//BC,AB=CD,AD=√2,E为CD中点，连接AE，且AE=2√3,∠DAE=30°，作AF⊥AE交BC于F，则BF=【 】
如图是一张长12cm，宽10cm的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形，剩余部分（阴影部分）可制成底面积24cm2是的有盖的长方体铁盒．则剪去的正方形的边长为______cm．
如图，四边形OABC是平行四边形，以点O为圆心，OC为半径的⊙O与AB相切于点B，与AO相交于点D，AO的延长线交⊙O于点E，连接EB交OC于点F，求∠C和∠E的度数．
平面内，将长分别为 1，5，1，1，d的线段，顺次首尾相接组成凸五边形(如图)，则d可能是【 】
如图是钉板示意图，每相邻4个钉点是边长为1个单位长的小正方形顶点，钉点A，B的连线与钉点 C，D的连线交于点E，则(1)AB与CD是否垂直?______(填是”或否")(2)AE=______.
如图，扇形纸片AOB的半径为3，沿AB折叠扇形纸片，点O恰好落在(AB) ̂上的C处，图中阴影部分的面积为【 】
下图是由5个完全相同的小正方体摆成的几何体，则这个几何体的主视图是【 】
一个由长方体截去一部分后得到的几何体如图水平放置，其俯视图是【 】