小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30°,同一时刻,根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为【 】

A、(6+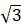 )米
)米
B、12米
C、 (4-2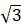 )米
)米
D、10米
小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30°,同一时刻,根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为【 】

A、(6+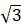 )米
)米
B、12米
C、 (4-2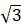 )米
)米
D、10米
A
小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为 60°,求山高【 】
在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD=________.
已知BD 垂直平分AC,∠BCD=∠ADF,AF⊥AC.(1)证明四边形ABDF是平行四边形;(2)若AF=DF=5,AD=6,求AC的长.
如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
如图,在RtΔABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为_______.
如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是【 】
如图所示,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是________.
如图,ΔABC中,点E在边AC上,EB=EA,∠A=2∠CBE,CD垂直于BE的延长线于点D,BD=8,AC=11,则边BC的长为_______.
已知三角形两边的长分别是4和10,则此三角形第三边的长可能是【 】
如图,在△ABC中,AB=AC,∠ABC=72°.(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标是(0,2),直线AC的解析式为y=1/2 x-1,则tanA的值是______.
如图,在△ABC中,点D、E分别是BC、AC的中点,AD与BE相交于点F,若BF=6,则BE的长是________.
如图,将△ABC折叠,使AC边落在△AB边上,展开后得到折痕l,则l是ABC的【 】