【图形定义】

有一条高线相等的两个三角形称为等高三角形，

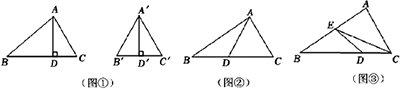
例如：如图①，在∆ABC和∆A'B'C'中，AD，A'D'分别是BC和B'C'边上的高线，且AD=A'D'、则∆ABC和∆A'B'C'是等高三角形。

【性质探究】

如图①，用S_∆ABC和S_∆A'B'C'分别表示∆ABC和∆A'B'C'的面积，

则S_∆ABC=1/2 BC∙AD,S_{∆A' B' C'}=1/2 B'C'∙A'D',

∵AD=A'D'

∴S_∆ABC:S_∆A'B'C'=BC:B'C'.

【性质应用】

(1)如图②，D是△ABC的边BC上的一点.若BD=3，DC=4，则S_∆ABD:S_∆ADC=________;

(2)如图③，在ΔABC中，D，E分别是BC和AB边上的点.若BE:AB=1:2,CD:BC=1:3,S_∆ABC=1,则S_∆BEC=______, S_∆DEC=________.

(3)如图③，在ΔABC中，D，E分别是BC和AB边上的点. 若BE:AB=1:m,CD:BC=1:n,S_∆ABC=a,则S_∆DEC=________.