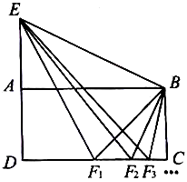
如图,四边形ABCD是矩形,延长DA到点E,使AE=DA,连接EB,点F1是CD的中点,连接EF1,BF1,得到ΔEF1B;点F2是CF_1的中点,连接EF2,BF2,得到ΔEF2 B;点F3是CF2的中点,连接EF3,BF3,得到ΔEF3 B;…;按照此规律继续进行下去,若矩形ABCD的面积等于2,则ΔEFn B的面积为_________.(用含正整数n的式子表示)
如图,四边形ABCD是矩形,延长DA到点E,使AE=DA,连接EB,点F1是CD的中点,连接EF1,BF1,得到ΔEF1B;点F2是CF_1的中点,连接EF2,BF2,得到ΔEF2 B;点F3是CF2的中点,连接EF3,BF3,得到ΔEF3 B;…;按照此规律继续进行下去,若矩形ABCD的面积等于2,则ΔEFn B的面积为_________.(用含正整数n的式子表示)

(2n+1)/2n
如图,在ΔABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D,若BC=4,则CD的长为_________.
下图是由全等的小正方形组成的图案,假设可以随意在图中取点,那么这个点取在阴影部分的概率是_________.
若关于x的一元二次方程x2+2x-k=0无实数根,则k的取值范围是_________.
若一次函数y=2x+2的图象经过点(3,m),则m=_________.
截至2020年3月底,我国已建成"5G" 基站198 000个,将数据198 000用科学记数法表示为_________.
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8,BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是【 】
如图,已知点O是△ABC的外心,∠A=40°,连结BO、CO则∠BOC的度数是【 】
如图,在△ABC中,点D、E分别是BC、AC的中点,AD与BE相交于点F,若BF=6,则BE的长是________.
如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB. (1)若AE=1,求△ABD的周长;(2)若AD=1/3 BD,求tan∠ABC的值.
如图,将△ABC折叠,使AC边落在△AB边上,展开后得到折痕l,则l是ABC的【 】
如图,在平面直角坐标系中,△AOB的边AO、AB的中点C、D的横坐标分别是1、4,则点B的横坐标是______.
如图,边长为1的正方形ABCD中,点E为AD的中点,连接BE,将ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
如图,已知∠BAC=60°,AD是角平分线且AD=10,作AD的垂直平分线交AC于点F,作DE⊥AC,则△DEF的周长为____________.