初中数学-中考试题(广东省广州市 2023年三视图)

单项选择（2023年广东省广州市）

一个几何体的三视图如图所示，则它表示的几何体可能是【】

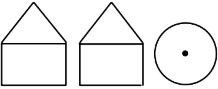
A、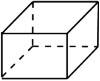

B、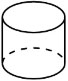

C、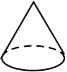

D、

答案解析

D

讨论

初中数学

-(-2023)=【】

垂中平行四边形的定义如下：在平行四边形中，过一个顶点作关于不相邻的两个顶点的对角线的垂线交平行四边形的一条边，若交点是这条边的中点，则该平行四边形是“垂中平行四边形”.(1)如图1所示，四边形ABCD为“垂中平行四边形”，AF=√5,CE=2，则AE=______;AB=______;(2)如图2，若四边形ABCD为“垂中平行四边形”，且AB=BD，猜想AF与CD的关系，并说明理由；(3)①如图3 所示，在△ABC中，BE=5,CE=2AE=12,BE⊥AC交AC于点E，请画出以 BC为边的垂中平行四边形，要求：点A在垂中平行四边形的一条边上(温馨提示：不限作图工具)；②若△ABC关于直线AC对称得到△AB'C，连接CB'，作射线CB'交①中所画平行四边形的边于点P,连接PE，请直接写出PE的值.

为了测量抛物线的开口大小，某数学兴趣小组将两把含有刻度的直尺垂直放置，并分别以水平放置的直尺和竖直放置的直尺为x,y轴建立如图所示平面直角坐标系，该数学小组选择不同位置测量数据如下表所示，设BD的读数为x，CD读数为y，抛物线的顶点为C.(1)(I)列表： ① ② ③ ④ ⑤ ⑥x 0 2 3 4 5 6y 0 1 2.25 4 6.25 9(Ⅱ)描点：请将表格中的(x,y)描在图2中；(Ⅲ)连线：请用平滑的曲线在图2将上述点连接，并求出y与x的关系式；(2)如图3所示，在平面直角坐标系中，抛物线y=a(x-h)²+k的顶点为C，该数学兴趣小组用水平和竖直直尺测量其水平跨度为AB，竖直跨度为CD，且AB=m,CD=n，为了求出该抛物线的开口大小，该数学兴趣小组有如下两种方案，请选择其中一种方案，并完善过程：方案一：将二次函数y=a(x-h)²+k平移，使得顶点C与原点O重合，此时抛物线解析式为y=ax².①此时点B'的坐标为________；②将点B'坐标代入y=ax²中，解得a=______；(用含m,n的式子表示).方案二：设C点坐标为(h,k).①此时点B的坐标为______；②将点B坐标代入y=a(x-h)²+k中，解得a=______；(用含m,n的式子表示).(3)【应用】如图4已知平面直角坐标系xOy中有A,B两点，AB=4，且AB//x轴，二次函数C1:y1=2(x+h)²+k和C2:y2=a(x+h)²+b都经过A,B两点，且C1和C2的顶点P,Q距线段AB的距离之为和10，求a的值.

如图，在△ABD中，AB=BD,⨀O为△ABD的外接圆，BE为⨀O的切线，AC为⨀O的直径，连接DC并延长BE于点E.(1) 求证：DE⊥BE；(2) 若AB=5√6,BE=5，求⨀O的半径.

【背景：缤纷618，优惠送大家】今年618各大电商平台促销火热，线下购物中心也亮出大招，年中大促进入“白热化”。深圳各大购物中心早在5月就开始推出618活动，进入6月更是持续加码，如图1，某商场为迎接即将到来的618优惠节，采购了若干辆购物车。【素材】如图为购物车叠放在一起的示意图2，若一辆购物车车身长lm，每增加一辆购物车，车身增加0.2m.解决问题：【任务1】若某商场采购了n辆购物车，求车身总长L与购物车辆数n的表达式；【任务2】若该商场用直立电梯从一楼运输该批购物车到二楼，已知该商场的直立电梯长为 2.6m，且一次可以运输两列购物车，求直立电梯一次性最多可以运输多少辆购物车?【任务3】若该商场扶手电梯一次性可以运输24辆购物车，若要运输100辆购物车，且最多只能使用电梯5次，求：共有多少种运输方案?

据了解，“i深圳”体育场地一键预约平是市委、市政府打造“民生幸福标杆”城市过程中，推动的惠民利民重要举措，在满足市民健身需求、激发全民健身热情、促进体育消费等方面具有重大意义。按照符合条件的学校体育场馆和社会体育场馆“应接尽接”原则，“i深圳”体育场馆一键预约平台实现了“让想运动的人找到场地，已有的体育场地得到有效利用”。小明爸爸决定在周六上午预约一所学校的操场锻炼身体，现有A，B两所学校适合，小明收集了这两所学校过去10周周六上午的预约人数:学校A：28，30，40，45，48，48，48，48，48，50学校B： (1)根据上述统计数据，填表：学校平均数众数中位数方差A ①____ 48 83.299B 48.4 ②____ ③____ 354.04(2)根据上述材料分析，小说爸爸应该预约哪所学校？请说明你的理由.

先化简，再求值：(1-2/(a+1))÷(a²-2a+1)/(a+1)，其中a=√2+1.

计算：-2cos45°+(π-3.14)0+|1-√2|+(1/4)-1.

如图，在△ABC中，AB=AC,tan∠B=5/12,D为BC上一点，且满足BD/CD=8/5，过D作DE⊥AD交AC延长线于点E，则CE/AC=______.

如图，在正面正解坐标系中，四边形AOCB为菱形，tan∠AOC=4/3,且点A落在反比例函数y=3/x上，点B落在反比例函数y=k/x(k≠0)上，则k=______.

三视图

下列图形中，主视图、左视图和俯视图相同的是【】

下列图形中，主视图和左视图一样的是【】

四个大小相同的正方体搭成的几何体如图所示，从正面看到的视图是【】

下列几何体中，俯视图为四边形的是【】

如图，由5个相同正方体组合而成的几何体，它的主视图是【】

如图，由4个相同正方体组合而成的几何体，它的左视图是【】

如图，正方形纸板的一条对角线垂直于地面，纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板，在灯光照射下，正方形纸板在地面上形成的影子的形状可以是【】

下图是由5个完全相同的小正方体摆成的几何体，则这个几何体的主视图是【】

由几个大小相同的正方形组成的几何图形如图，则它的俯视图是【】

下列图形是某几何体的三视图(其中主视图也称正视图，左视图也称侧视图)。已知主视图和左视图是两个全等的矩形.若主视图的相邻两边长分别为2和3，俯视图是直径等于2的圆，则这个几何体的体积为________.

几何图形

下列出版社的商标图案中，是轴对称图形的为【】

如图，街道AB与CD平行，拐角∠ABC=137°，则拐角∠BCD = 【】

如图，AB是⊙O的直径，∠BAC=50°,则∠D=【】

边长分别为10，6，4的三个正方形拼接在一起，它们的底边在同一直线上(如图)，则图中阴影部分的面积为________.

如图，在▱ABCD 中，∠DAB=30°.(1)实践与操作：用尺规作图法过点D作AB边上的高DE；(保留作图痕迹，不要求写作法)(2)应用与计算：在(1)的条件下，AD=4，AB=6，求BE的长.

综合与实践主题：制作无盖正方体形纸盒.素材：一张正方形纸板步骤1：如图1，将正方形纸板的边长三等分，画出九个相同的小正方形，并剪去四个角上的小正方形；步骤2：如图2，把剪好的纸板折成无盖正方体形纸盒. 猜想与证明:(1)直接写出纸板上∠ABC 与纸盒上∠A1B1C1的大小关系:(2)证明 (1)中你发现的结论.

综合探究如图1，在矩形ABCD中（AB>AD），对角线AC,BD相交于点O，点A关于BD的对称点为A'.连接AA'交BD于点E，连接CA'. (1)求证：AA'⊥CA'；(2)以点O为圆心，OE为半径作圆.①如图2，⨀O与CD相切，求证：AA'=√3 CA'；②如图3，⨀O与CA'相切，AD=1，求⨀O的面积.

下列图形中具有稳定性的是【】

如图，直线a，b被直线c所截，a//b，∠1=40°，则∠2等于【】

如图，在△ABC中，BC=4，点D、E分别为AB、AC的中点，则DE=【】