综合探究
如图1,在矩形ABCD中(AB>AD),对角线AC,BD相交于点O,点A关于BD的对称点为A'.连接AA'交BD于点E,连接CA'.
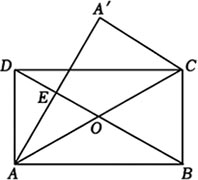

(1)求证:AA'⊥CA';
(2)以点O为圆心,OE为半径作圆.
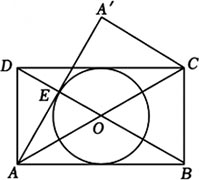
①如图2,⨀O与CD相切,求证:AA'=√3 CA';
②如图3,⨀O与CA'相切,AD=1,求⨀O的面积.
综合探究
如图1,在矩形ABCD中(AB>AD),对角线AC,BD相交于点O,点A关于BD的对称点为A'.连接AA'交BD于点E,连接CA'.



(1)求证:AA'⊥CA';
(2)以点O为圆心,OE为半径作圆.
①如图2,⨀O与CD相切,求证:AA'=√3 CA';
②如图3,⨀O与CA'相切,AD=1,求⨀O的面积.
(1)∵点A关于BD的对称点为A',∴AE=A' E,AA'⊥BD,∵ABCD是矩形,∴OA=OC,∴OE//A'C,∴AA'⊥A'C.(2)①如图,设⨀O与CD切于点F,连接并延长FO交AB于点G,∵圆心O为矩形ABCD两对角线的交点,∴⨀O与AB切于点G,∴∠EAO=∠GAO=∠GBO,而∠EAO+∠GAO+∠GBO=∠EAB+∠EBA=90°,∴∠EAO=30°,∴(CA')/AA'=tan30°=√3,即AA'=√3 CA';②如图,设⨀...
查看完整答案如图,AB是⨀O的直径,BC是⨀O的弦,先将 沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若=,设∠ABC=α,则α所在的范围是【 】
如图,ABAB是⨀O的直径,C,D是⨀O上两点,C是的中点.过点C作AD的垂线,垂足是E.连接AC交BD于点F.(1)求证:CE是⨀O的切线;(2)若DC/DF=,求cos∠ABD的值.
如图,四边形ABCD内接于⨀O,∠1=∠2,延长BC到点E,使得CE=AB,连接ED.(1)求证:BD=ED;(2)若AB=4,BC=6,∠ABC=60°,求tan∠DCB的值.
如图,FA、GB、HC、ID、JE是五边形ABCDE的外接圆的切线,则∠BAF+∠CBG+∠DCH+∠EDI+∠AEJ=______.
如图,已知P是⊙O外一点.用两种不同的方法过点P作⊙O的一条切线.要求:(1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.
如图,AB是⊙O的直径,点C为圆上一点,AC=3,∠ABC的平分线交AC于点D,CD=1,则⊙O的直径为【 】
如图,AB为⨀O的弦,D,C为弧ACB的三等分点,AC//BE. (1)求证:∠A=∠E;(2)若BC=3,BE=5,求CE的长.
如图,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD = 【 】
边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为________.
如图,在▱ABCD 中,∠DAB=30°.(1)实践与操作:用尺规作图法过点D作AB边上的高DE;(保留作图痕迹,不要求写作法)(2)应用与计算:在(1)的条件下,AD=4,AB=6,求BE的长.
如图,在△ABC中,点D、E分别是BC、AC的中点,AD与BE相交于点F,若BF=6,则BE的长是________.
如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB. (1)若AE=1,求△ABD的周长;(2)若AD=1/3 BD,求tan∠ABC的值.
如图,边长为1的正方形ABCD中,点E为AD的中点,连接BE,将ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.