初中数学-中考试题(广东省 2023年圆的概念与性质)

单项选择（2023年广东省）

如图，AB是⊙O的直径，∠BAC=50°,则∠D=【】

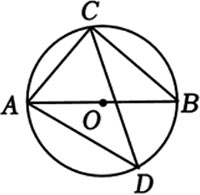
A、20°

B、40°

C、50°

D、80°

答案解析

B

讨论

几何图形

下列出版社的商标图案中，是轴对称图形的为【】

如图，街道AB与CD平行，拐角∠ABC=137°，则拐角∠BCD = 【】

边长分别为10，6，4的三个正方形拼接在一起，它们的底边在同一直线上(如图)，则图中阴影部分的面积为________.

如图，在▱ABCD 中，∠DAB=30°.(1)实践与操作：用尺规作图法过点D作AB边上的高DE；(保留作图痕迹，不要求写作法)(2)应用与计算：在(1)的条件下，AD=4，AB=6，求BE的长.

综合与实践主题：制作无盖正方体形纸盒.素材：一张正方形纸板步骤1：如图1，将正方形纸板的边长三等分，画出九个相同的小正方形，并剪去四个角上的小正方形；步骤2：如图2，把剪好的纸板折成无盖正方体形纸盒. 猜想与证明:(1)直接写出纸板上∠ABC 与纸盒上∠A1B1C1的大小关系:(2)证明 (1)中你发现的结论.

综合探究如图1，在矩形ABCD中（AB>AD），对角线AC,BD相交于点O，点A关于BD的对称点为A'.连接AA'交BD于点E，连接CA'. (1)求证：AA'⊥CA'；(2)以点O为圆心，OE为半径作圆.①如图2，⨀O与CD相切，求证：AA'=√3 CA'；②如图3，⨀O与CA'相切，AD=1，求⨀O的面积.

平面内，将长分别为 1，5，1，1，d的线段，顺次首尾相接组成凸五边形(如图)，则d可能是【】

如图是钉板示意图，每相邻4个钉点是边长为1个单位长的小正方形顶点，钉点A，B的连线与钉点 C，D的连线交于点E，则(1)AB与CD是否垂直?______(填是”或否")(2)AE=______.

如图，扇形纸片AOB的半径为3，沿AB折叠扇形纸片，点O恰好落在(AB) ̂上的C处，图中阴影部分的面积为【】

如图，在矩形ABCD中，AC是对角线.(1)实践与操作：利用尺规作线段AC的垂直平分线，垂足为点O，交边AD干点E，交边BC于点F(要求：尺规作图并保留作图痕迹，不写作法，标明字母).(2)猜想与证明：试猜想线段AE与CF的数量关系，并加以证明.

圆的概念与性质

如图，已知在△ABC中，∠ABC<90°，AB≠BC，BE是AC边上的中线.按下列步骤作图：①分别以点BC为圆心，大于线段BC长度一半的长为半径作弧，相交于点M,N;②过点M,N作直线MN，分别交BC,BE于点D,O;③连结CO,DE则下列结论错误的是【】

如图，AB是⊙O的弦，C是AB的中点，OC交AB于点D.若AB=8cm,CD=2cm，则⊙O的半径为______cm.

如图，正六边形ABCDEF内接于⨀O.点M在(AB) ̂上则∠CME的度数为【】

如图所示，该小组发现8米高旗杆DE的影子 EF 落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在圆的半径的活动.小刚身高 1.6 米，测得其影长2.4米，同时测得 EG的长为3米，HF 的长为1米，测得拱高(弧 GH 的中点到弦 GH 的距离即MN的长)为2米，求小桥所在圆的半径.

如图，在平面直角坐标系中，⊙M过原点O，与x轴交于A(4，0)，与y轴交于B(0，3)，点C为劣弧AO的中点，连接AC 并延长到D，使DC=4CA，连接BD.(1)求OM的半径；(2)证明：BD为⊙M的切线；(3)在直线MC上找一点P，使|DP-AP|最大.

如图，AB为⊙O的直径，已知∠DCB=20°，则∠DBA为【】

如图，A、B、C是⊙O上的三个点，∠ABC=25°，则∠AOC=________.

如图，等边△ABC的三个顶点都在⨀O上，AD是⨀O的直径.若OA=3，则劣弧BD的长是【】

如图，在⊙O中，点A在弧BC上，∠BOC=100°,则∠BAC=__________.

如图1，在四边形ABCD中，AD// BC，∠DAB=90°，AB是⊙O的直径，CO平分∠BCD.（1）求证：直线CD与⊙O相切；（2）如图2，记（1）中的切点为E，P为优弧AE上一点，AD=1，BC=2.求tan⁡∠ APE的值.

圆

已知⊙O的半径为7，AB是⊙O的弦，点P在弦AB上．若PA＝4，PB＝6，则 OP＝【】

如图1，水平放置一个三角板和一个量角器，三角板的边AB和量角器的直径DE在一条直线上，AB=BC=6cm，OD=3cm，开始的时候BD=1cm，现在三角板以2cm/s 的速度向右移动.(1)当B与O重合的时候，求三角板运动的时间；(2)如图2，当AC与半圆相切时，求AD；(3)如图3，当AB和DE 重合时，连接CO交半圆于点F，连接并延长DF交CE于点G，求证：CF²=CG·CE.

如图，已知AB=AC=5,BC=3，以A,B两点为圆心，大于1/2 AB的长为半径画圆弧，两弧相交于两点M,N，连接MN与AC相交于点D，则△BCD的周长为【】

如图，在⊙O中，圆心角∠AOB=120°，弦AB=2cm，则OA=_______cm.

如图（左），已知在⊙O中，点C为劣弧AB上的中点，连接AC并延长至D，使CD=CA，连接DB并延长DB交⊙0于点E，连接AE.(1)求证：AE是⊙O的直径;(2)如图（右），连接EC，⊙O半径为5，AC的长为4，求阴影部分的面积之和.(结果保留T与根号)

如图，⊙C过原点，且与两坐标轴分别交于点A、点B，点A的坐标为(0，3)，M是第三象限内上一点，∠BMO=120°，则⊙C的半径长为【】

如图，正方形ABCD的边长为4，点E是边BC上一点，且BE=3，以点A为圆心，3为半径的圆分别交AB,AD于点F,G,DF与AE交于点H.并与⨀A交于点K，连接HG,HC.给出下列四个结论，其中正确的有________（填写所有正确结论的序号）(1) H是FK的中点； (2) △HGD≅△HEC；(3) S△AHG:S△DHC=9:16; (4) DK=7/5

如图，PA,PB是⊙O的切线，A,B是切点.若∠P=50°，则∠AOB=________.

如图，⊙O是△ABC的外接圆，AD是⊙O的直径，AD⊥BC于点E.(1)求证：∠BAD=∠CAD；(2)连接并延长OB，交AC于点F，交⊙O于点G，连接GC.若⊙O的半径为5，OE=3,求GC和OF的长.

在平面直角坐标系xOy中，⊙O的半径为1.对于点A和线段BC，给出如下定义：若将线段BC绕点A旋转可以得到⊙O的弦B'C'(B',C'分别是BC的对应点)，则称线段BC是⊙O的以点A为中心的“关联线段”.(1)如图，点A，B1，C1，B2，C2，B3，C3的横、纵坐标都是整数，在线段B1C1，B2C2， B3C3中，⊙O的以点A为中心的“关联线段”是__________;(2)△ABC是边长为1的等边三角形，点A(0，t)，其中t≠0.若BC是⊙O的以点A为中心的“关联线段”，求t的值；(3)在△ABC中，AB=1，AC=2.若BC是△O的以点A为中心的“关联线段”，直接写出OA的最小值和最大值，以及相应的BC长。