-
关注“优题吧”，分配平台账号.
题吧，智能辅助学习中心
中考2016年广东省广州市( )
解不等式组
，并在数轴上表示解集.
解答过程见word版
中考2018年广东省广州市( )
友谊商店A型号笔记本电脑的售价是a元/台.最近，该商店对A型号笔记本电脑举行促销活动，有两种优惠方案.方案一：每台按售价的九折销售;方案二：若购买不超过5台，每台按售价销售；若超过5台，超过的部分每台按售价的八折销售，某公司一次性从友谊商店购买A型号笔记本电脑x台.
(1)当x=8时，应选择哪种方案，该公司购买费用最少?最少费用是多少元?
(2)若该公司采用方案二购买更合算，求x的取值范围.
(1)当x=8时，方案一的费用是：0.9ax=0.9a×8=7.2a；
方案二的费用是：5a+0.8a(x-5)=5a+0.8a×(8-5)=7.4a.
∵a>0，
∴7.2a<7.4a.
答：应选择方案一，最少费用是7.2a元.
(2)设方案一、二的费用分别为W1,W2，
由题意可得：W1=0.9ax.
当0≤x≤5时，W2=ax；
当x>5时，W2=5a+(x-5)×0.8a=0.8ax+a，
由题意可得：W1>W2，
∵当0≤x≤5时，W2=ax>W1，不合题意，
∴0.8ax+a<0.9ax，
解得x>10且x为正整数，
即该公司采用方案二购买更合算，x的取值范围为x>10且x为正整数.
中考2018年广东省广州市( )
解不等式组：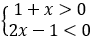
解不等式①，可得：x>-1，
解不等式②，可得：x<2，
故不等式组的解集为：-1<x<2.
中考2020年广东省广州市( )
解不等式组：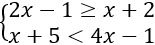
由①式得：x≥3，
由②式得：x>2,
故原不等式组的解集为：x≥3.
中考2022年广东省广州市( )
解不等式：3x-2<4
移项得：3x<4+2,
合并同类项得：3x<6,
系数化为1得：x<2.