初中数学-中考试题(山西省 2022年直角三角形)

问答题（2022年山西省）

问题情境:在Rt△ABC中，∠BAC=90°，AB=6，AC=8.直角三角板EDF中∠EDF=90°，将三角板的直角顶点D放在Rt△ABC斜边BC的中点处，并将三角板绕点D旋转，三角板的两边DE，DF分别与边AB，AC交于点M，N.猜想证明：

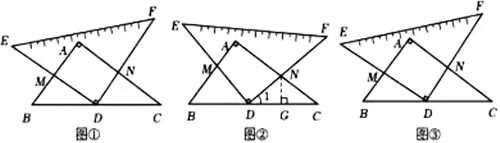
(1)如图①，在三角板旋转过程中，当点M为边AB的中点时，试判断四边形AMDN的形状，并说明理由.

问题解决：

(2)如图②，在三角板旋转过程中，当∠B=∠MDB时，求线段CN的长;

(3)如图③，在三角板旋转过程中，当AM=AN时，直接写出线段AN的长.

答案解析

(1)四边形AMDN为矩形.理由如下：∵M为AB的中点，D为BC的中点，∴MD//AC又AC⊥AB，∴MD⊥AB,∠AMD=90°∴∠A=∠AMD=∠MDN=90°∴四边形AMDN为矩形.(2)在Rt△ABC中，∠A=90°,AB=6,AC=8,∴BC=10,∵D是BC的中点，∴CD=1/2 BC=5.∵∠MDB+∠1=90°,∠MDB=∠B,∠B+∠C=90°∴∠1=∠C∴ND=NC.过点N作NG⊥BC于点G,则CG=1/2 CD=5/2.易知△CGN∼△CAB,∴CG/CA=CN/CB，解得: ...

查看完整答案

讨论

旋转

如图，在正方形ABCD中，AB=3，点E，F分别在边AB，CD上，∠EFD=60°.若将四边形EBCF沿EF折叠，点B恰好落在AD边上，则BE的长度为【】

如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，则下列四个图形中正确的是【】

如图，在边长为6的正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，将ΔADF绕点A顺时针旋转90°得到ΔABG.若DF=3，则BE的长为__________.

如图的四个三角形中，不能由△ABC经过旋转或平移得到的是【】

在△ABC中，∠ACB＝90°，CD是中线，AC＝BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E、F，DF与AC交于点M，DE与BC交于点N．（1）如图1，若CE＝CF，求证：DE＝DF；（2）如图2，在∠EDF绕点D旋转的过程中，试证明CD2＝CE•CF恒成立；（3）若CD＝2，CF＝，求DN的长．

如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在某个点上，在建立平面直角坐标系后，点A的坐标为(-6，1)，点B的坐标为(-3，1)点C的坐标为(-3，3).(1)将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1，试在图上画出的图形Rt△A1B1C1，并写出点A1的坐标；(2)将原来的R△ABC绕点B顺时针旋转90°得到Rt△A2B2C2，试在图上画出Rt△A2B2C2的图形.

如图，在△ABC中，AB=AC，若M是BC边上任意一点，将△ABM绕A逆时针旋转得到△ACN，点M的对应点为点N，连接MN，则下列结论一定正确的是【】

将一个矩形纸片OABC放置在平面直角坐标系中，点O(0,0),A(3,0),C(0,6)，点P在边OC上(点P不与点O,C重合)，折叠该纸片，使折痕所在的直线经过点P，并与x轴的正半轴相交于点Q,且∠OPQ=30°，点O的对应点O'落在第一象限.设OQ=t. (I)如图①，当t=1时，求∠O'QA的大小和点O'的坐标:(Ⅱ)如图②，若折叠后重合部分为四边形，O' Q,O'P分别与边AB相交于点E,F，试用含有t的式子表示O'E的长，并直接写出t的取值范围:(Ⅲ)若折叠后重合部分的面积为3√3，则t的值可以是__________(请直接写出两个不同的值即可).

如图，将ΔABC先向右平移3个单位，再绕原点O旋转180°得到ΔA'B'C'，则点A的对应点A'的坐标是【】

如图，在Rt△ABC中，∠ACB=90°,AB=5cm,BC=3cm，将△ABC绕点A按逆时针方向旋转90°得到△ADE，连接CD.点P从点B出发，沿BA方向匀速运动,速度为1cm/s，同时，点Q从点A出发，沿AD方向匀速运动，速度为1m/s. PQ交AC于点F，连接CP,EQ，设运动时间为t(s)(0<t<5).解答下列问题：(1)当EQ⊥AD时，求t的值;(2)设四边形PCDQ的面积为S(cm^2)，求S与t之间的函数关系式;(3)是否存在某一时刻t，使PQ//CD?若存在，求出t的值；若不存在，请说明理由.

直角三角形

图①是甘肃省博物馆的镇馆之宝——铜奔马，又称“马踏飞燕”，于1969年10月出土于武威市的雷台汉墓，1983年10月被国家旅游局确定为中国旅游标志.在很多旅游城市的广场上都有“马踏飞燕”雕塑.某学习小组把测量本城市广场的“马踏飞燕”雕塑（图②）最高点离地面的高度作为一次课题活动，同学们制定了测量方案，并完成了实地测量，测得结果如下表：课题测量“马踏飞燕”雕塑最高点离地面的高度测量示意图如图，雕塑的最高点B到地面的高度为BA，在测点C用仪器测得点B的仰角为α，前进一段距离到达测点E，再用该仪器测得点B的仰角为β，且点A，B，C，D，E，F均在同一竖直平面内，点A，C，E在同一条直线上.α的度数β的度数CD的长度仪器CD（EF）的高度测量数据31°42°5米1.5米请你根据上表中的测量数据，帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度（结果保留一位小数）.（参考数据：sin⁡3 1°≈0.52，cos⁡3 1°≈0.86，tan⁡3 1°≈0.60，sin⁡4 2°≈0.67，cos⁡4 2°≈0.74，tan⁡4 2°≈0.90）

有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，∠ABC=90°，点M，N分别在射线BA，BC上，MN长度始终保持不变，MN=4，E为MN的中点，点D到BA，BC的距离分别为4和2.在此滑动过程中，猫与老鼠的距离DE的最小值为_________.

如图，RtΔABC中，∠C=90°，利用尺规在BC，BA上分别截取BE，BD，使BE=BD；分别以D，E为圆心、以大于1/2 DE的长为半径作弧，两弧在∠CBA内交于点F；作射线BF交AC于点G．若CG=1，P为AB上一动点，则GP的最小值为【】

如图，ΔABC中，点E在边AC上，EB=EA，∠A=2∠CBE，CD垂直于BE的延长线于点D，BD=8，AC=11，则边BC的长为_______．

脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高AB所在的直线．为了测量房屋的高度，在地面上C点测得屋顶A的仰角为35°，此时地面上C点、屋檐上E点、屋顶上A点三点恰好共线，继续向房屋方向走8m到达点D时，又测得屋檐E点的仰角为60°，房屋的顶层横梁EF=12m，EF//CB，AB交EF于点G（点C，D，B在同一水平线上）。（参考数据：sin⁡3 5°≈0.6，cos⁡3 5°≈0.8，tan⁡3 5°≈0.7，≈1.7）（1）求屋顶到横梁的距离AG；（2）求房屋的高AB（结果精确到1m）．

如图，在△ABC中，∠C=90°,tan⁡A=/3,∠ABC的平分线BD交AC于点D.CD=.求AB的长？

如图，在RtΔABC中，∠ACB=90°，AC=BC=2，CD⊥AB于点D.点P从点A出发，沿A→D→C的路径运动，运动到点C停止，过点P作PE⊥AC于点E，作PF⊥BC于点F.设点P运动的路程为x，四边形CEPF的面积为y，则能反映y与x之间函数关系的图象是【】

如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路，现新修一条路AC到公路l，小明测量出∠ACD=30°，∠ABD=45°，BC=50m，请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据：≈1.414，≈1.732)

小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上，如图，此时测得地面上的影长为8米，坡面上的影长为4米，已知斜坡的坡角为30°，同一时刻，根长为1米且垂直于地面放置的标杆在地面上的影长为2米，则树的高度为【】

如图， RT△ABC中∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5,OC=6，则另一直角边BC的长为________.

三角形

如图，在△ABC中，点D、E分别是BC、AC的中点，AD与BE相交于点F，若BF=6，则BE的长是________.

我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为a,b,c，记p=(a+b+c)/2，则其面积S=.这个公式也被称为海伦-秦九韶公式.若p=5,c=4，则此三角形面积的最大值为【】

【图形定义】有一条高线相等的两个三角形称为等高三角形，例如：如图①，在∆ABC和∆A'B'C'中，AD，A'D'分别是BC和B'C'边上的高线，且AD=A'D'、则∆ABC和∆A'B'C'是等高三角形。【性质探究】如图①，用S∆ABC和S∆A'B'C'分别表示∆ABC和∆A'B'C'的面积，则S∆ABC=1/2 BC∙AD,S∆A' B' C'=1/2 B'C'∙A'D',∵AD=A'D'∴S∆ABC:S∆A'B'C'=BC:B'C'.【性质应用】(1)如图②，D是△ABC的边BC上的一点.若BD=3，DC=4，则S∆ABD:S∆ADC=________;(2)如图③，在ΔABC中，D，E分别是BC和AB边上的点.若BE:AB=1:2,CD:BC=1:3,S∆ABC=1,则S∆BEC=______, S∆DEC=________.(3)如图③，在ΔABC中，D，E分别是BC和AB边上的点. 若BE:AB=1:m,CD:BC=1:n,S∆ABC=a,则S∆DEC=________.

如图，将△ABC折叠，使AC边落在△AB边上，展开后得到折痕l，则l是ABC的【】

如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为a，β，则正确的是【】

题目:“如图，∠B=45°，BC=2，在射线BM上取一点A，设AC=d，若对于d的一个数值，只能作出唯一一个△ABC，求d的取值范围.”对于其答案，甲答：d≥2；乙答：d=1.6；丙答：d=√2，则正确的是【】

如图，在ΔABC中，D是BC边上一点，且BD=BA. （1）尺规作图（保留作图痕迹，不写作法）：①作∠ABC的角平分线交AD于点E；②作线段DC的垂直平分线交DC于点F.（2）连接EF，直接写出线段EF和AC的数量关系及位置关系.

在ΔABC中，∠ABC=90°，AB=2，BC=3，点D为平面上一个动点，∠ADB=45°，则线段CD长度的最小值为________.

如图，某水渠的横断面是以AB为直径的半圆O，其中水面截线MN//AB.嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°，点M的俯角为7°.已知爸爸的身高为1.7m. (1)求∠C的大小及AB的长;(2)请在图中画出线段DH，用其长度表示最大水深(不说理由)，并求最大水深约为多少米(结果保留小数点后一位).(参考数据: tan76°取4，√17取4.1)

图①是某车站的一组智能通道闸机，当行人通过时智能闸机会自动识别行人身份，识别成功后，两侧的圆弧翼闸会收回到两侧闸机箱内，这时行人即可通过．图②是两圆弧翼展开时的截面图，扇形ABC和DEF是闸机的“圆弧翼”，两圆弧翼成轴对称，BC和EF均垂直于地面，扇形的圆心角∠ABC=∠DEF=28°，半径BA=ED=60cm，点A与点D在同一水平线上，且它们之间的距离为10cm．（1）求闸机通道的宽度，即BC与EF之间的距离（参考数据：sin⁡28°≈0.47，cos⁡28°≈0.88，tan⁡28°≈0.53）；（2）经实践调查，一个智能闸机的平均检票速度是一个人工检票口平均检票速度的2倍，180人的团队通过一个智能闸机口比通过一个人工检票口可节约3分钟，求一个智能闸机平均每分钟检票通过的人数．