设x,y是实数,则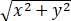 有最小值和最大值【 】
有最小值和最大值【 】
(1) (x-1)2+(y-1)2=1 (2) y=x+1
A、条件(1)充分,但条件(2)不充分
B、条件(2)充分,但条件(1)不充分
C、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D、条件(1)充分,条件(2)也充分
E、条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
设x,y是实数,则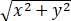 有最小值和最大值【 】
有最小值和最大值【 】
(1) (x-1)2+(y-1)2=1 (2) y=x+1
A、条件(1)充分,但条件(2)不充分
B、条件(2)充分,但条件(1)不充分
C、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D、条件(1)充分,条件(2)也充分
E、条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
A
设f(x)=x3+log2(x+),对任意实数a,b,a+b≥0是f(a)+f(b)≥0的【 】.
给定整数n≥2,设M0 (x0,y0)是抛物线y2=nx-1与直线y=x的一个交点.试证明对任意正整数m,必存在整数k≥2,使(x0m,y0m)为抛物线y2=kx-1与直线y=x的一个交点.
设{an}是公差不为0的无穷等差数列,则“{an}为递增数列”是“存在正整数N0,当n>N0时,an>0”的【 】
若xy≠0,则“x+y=0”是“y/x+x/y=-2”的【 】
设 a, b 为单位向量, 且 |a + b| = 1, 则 |a − b| =__________.
已知 α, β ∈ R, 则“存在 k ∈ Z 使得 α = kπ + (−1)kβ”是“sin α = sin β”的【 】
设 a ∈ R, 则“a > 1”是“a2 > a”的【 】
已知空间中不过同一点的三条直线 l, m, n, 则“l, m, n 在同一个平面”是“l, m, n 两两相交”的【 】
A:四边形ABCD为平行四边形.B:四边形ABCD为矩形.则A是B的________条件.
A:a=3;B:|a|=3,则A是B的__________条件.
A:θ=150°;B:sinθ=1/2,则A是B的__________条件.
设甲是乙的充分条件,乙是丙的充要条件,丙是丁的必要条件,那么丁是甲的【 】
已知E,F,G,H为空间中的四个点,设命题甲:点E,F,G,H不共面,命题乙:直线EF和GH不相交.那么【 】
已知h>0.设命题甲为:两个实数a,b满足|a-b|<2h;命题乙为:两个实数a,b满足|a-1|<h且|b-1|<h.那么【 】