设5π<θ<6π,cos(θ/2)=a，那么sin(θ/4)等于【 】
A、-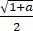 
B、- 
C、- 
D、-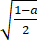 
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
已知z1,z2是两个给定的复数，且z1≠z2，它们在复平面上分别对应于点Z1和点Z2.如果z满足方程|z-z1|-|z-z2|=0,那么z对应的点Z的集合是【 】
设全集I为自然数集N，E={2n|n∈N}，F={4n|n∈N}，那么集合N可以表示成【 】
在直角坐标系xOy中，参数方程（其中t参数）表示的曲线是【 】
双曲线的中心在坐标原点O，焦点在x轴上，过双曲线右焦点且斜率为的直线交双曲线于P,Q两点.若OP⊥OQ,|PQ|=4，求双曲线的方程.
已知n为自然数，实数a>1，解关于x的不等式logax - 4loga2x + 12loga3x + ⋯ + n(-2)n-1loganx > (1-(-2)n)/3·loga(x2 - a).
根据函数单调性的定义，证明函数f(x)=-x3 + 1在(-∞,+∞)是减函数.
如图，已知ABCD是边长为4的正方形，E,F分别是AB,AD的中点，GC垂直于ABCD所在的平面，且GC=2.求点B到平面EFG的距离.
在△ABC中，已知cosA=-3/5，则sin(A/2)=______.
设α角属于第Ⅱ象限，且|cos α/2|=-cos α/2，则α/2角属于【 】
已知sinα=4/5，并且α是第二象限的角，那么tanα的值等于【 】
函数 y = cos4x - sin4x 的最小正周期是【 】
若α∈(0,π/2),tan2α=cosα/(2-sinα)，则tanα=【 】
已知f(x)=3sinx+2，对任意的x1∈[0,π/2]，都存在x2∈[0,π/2]，使得f(x1)=2f(x2+θ)+2成立，则下列选中θ可能的值是【 】
设函数f(x)=sin(ωx+π/3)在区间(0,π)恰有三个极值点、两个零点，则ω的取值范围是【 】
记函数f(x)=cos(ωx+φ) (ω>0,0<φ<π)的最小正周期为T，若f(T)=√3/2，x=π/9为f(x)的零点，则ω的最小值为____________．
记△ABC的内角A,B,C对应的边分别为a,b,c，已知sinC=√2 cosB,a²+b²-c²=√2 ab.(1) 求B；(2) 若△ABC的面积为3+√3，求c.
已知sinθ=-3/5,3π<θ<7π/2，求tanθ/2的值.
已知tanx=a，求(3sinx+sin3x)/(3cosx+cos3x)的值.
如果|cosθ|=1/5,5π/2<θ<3π，那么sin(θ/2)的值等于【 】
已知tanθ<0,cos(π/2+θ)=√5/5，则cosθ的值为【 】
设 A+B + C =180°，试证 sin2A +sin2B +sin2C = 4sinAsinBsinC.