高中数学-高考试题(全国统考 1991年双曲线)

问答题（1991年全国统考）

双曲线的中心在坐标原点O，焦点在x轴上，过双曲线右焦点且斜率为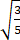的直线交双曲线于P,Q两点.若OP⊥OQ,|PQ|=4，求双曲线的方程.

答案解析

设双曲线的方程为x2/a2 -y2/b2 =1.依题意，点P,Q的坐标满足方程组(其中c=)，整理得(5b2-3a2 ) x2+6a2 cx-(3a2 c2+5a2 b2 )=0. ③设方程③的两个根为x1,x2，若5b2-3a2=0，则b/a=,即直线②与双曲线①的两条渐近线中的一条平行，故与双曲线只能有一个交点，与题设矛盾.所以5b2-3a2≠0.根据根与系数的关系，有由于P,Q在直线y= (x-c)上，可记为P(x1,(x1-c)),Q(x2, (x2-c)).由OP⊥OQ得( (x1-c))/x1 ∙( (x...

查看完整答案

讨论

圆锥曲线

造型可以做成美丽的丝带，将其看作图中曲线C的一部分.已知C过坐标原点O，且C上的点满足：横坐标大于-2，到点F(2,0)的距离与到定直线x=a(a<0)的距离之积为4，则【】

已知方程 kx2+y2=4 ，其中k为实数。对于不同范围的k值，分别指出方程所代表图形的类型，并画出显示其数量特征的草图．

已知F1,F2为椭圆C:x2/16+y2/4=1的两个焦点，P,Q为C上关于坐标原点对称的两点，且|PQ|=|F1F2 |，则四边形PF1QF2的面积为________.

设B是椭圆C:x2/5+y2=1的上顶点，点P在C上，则|PB|的最大值为【】

已知Γ:x2/2+y2=1,F1,F2是其左、右焦点，直线l过点P(m,0)(m≤-)，交椭圆于A,B两点，且A,B在x轴上方，点A在线段BP上.(1)若B是上顶点，||=||，求m的值;(2)若∙=1/3，且原点O到直线l的距离为4/15，求直线l的方程;(3)证明：对于任意m<-，使得//的直线有且仅有一条.

已知椭圆x2/a2 +y2/b2 =1(a>b>0)的右焦点为F，上顶点为B，离心率为(2√5)/5，且|BF|=√5.(1)求椭圆的方程；(2)直线l与椭圆有唯一的公共点M，与y轴的正半轴交于点N，过N与BF垂直的直线交x轴于点P，若MP//BF，求直线l的方程.

英：Find the equation to the normal to hyperbola x2/a2 -y2/b2 =1 at the point (x1,y1) . 汉：求双曲线x2/a2 -y2/b2 =1在点(x1,y1)处的法线方程.

The point of contact of a tangent to an hyperbola is midway between the points in which the tangent meets the asymptotes.

双曲线之切线与渐近线相交，试证切点移动其所包围之三角形之面积为常数.

Reduce the hyperbola 4x² - 9y² - 24x + 36y - 36 = 0 to standard form.

双曲线

双曲线x²/100-y²/64=1的焦点为S,S1;，其中S位于x正半轴上. P为双曲线在第一象限上的一点，记∠SPS1=α,α<π/2. 过点S且斜率与双曲线在P点切线相同的直线，与直线S1 P交于P1点，记P到直线SP1的距离为δ,β=S1 P.则不超过βδ/9 sin⁡α/2的最大整数为______.

于双曲线4/3 (x-2)2-(y+1)2=1中,已知其一直径之斜度为1/3，试求此直径及其共轭直径之方程式，若以此二共轭直径为新坐标轴,试求双曲线之新方程式.

有圆锥曲线方程式为 5x² -4y² - 20x - 24y + 4= 0，试求其中心、焦点、渐近线、准线.

试证双曲线之两渐近线及任一切线所成之三角形之面积等于一常数.

设双曲线x²/a² -y²/b² =1(a>0,b>0)的左右焦点分别为F1,F2，过F2作平等于y轴的直线交C于A,B两点，若|F1A|=13,|AB|=10，则C的离心率为______.

已知双曲线C的中心坐标为原点，左焦点为(-2√5,0)，离心率为√5.(1)求C的方程；(2)记C的左、右顶点分别为A1,A2，过点(-4,0)的直线与C的左支交于M,N两点，M在第二象限，直线MA1与NA2交于点P，证明：点P在定直线上.

已知方程x2/(2+λ)-y2/(1+λ)=1表示双曲线，求λ的取值范围.

双曲线y2/16 - x2/9=1的准线方程是__________.

双曲线2mx2 - my2 = 2的一条准线是y=1，则m=______.

双曲线x2/4 - y2/5=1的右焦点到直线x+2y-8=0的距离为______.

平面解析几何

△ABC 中, sin2A − sin2B − sin2C = sinBsinC.(1) 求 A;(2) 若 BC = 3, 求 △ABC 周长的最大值.

已知单位向量 a, b 的夹角为 60°, 则下列向量中, 与 b 垂直的是【】

△ABC 的内角 A, B, C 的对边分别为 a, b, c, 已知 cos2(π/2 + A) + cos A = 5/4.(1) 求 A.(2) b − c =/3a, 证明: △ABC 是直角三角形.

在平面内, A, B 是两个定点, C 是动点. •= 1, 则点 C 的轨迹为【】

在 △ABC 中, cosC =2/3, AC = 4, BC = 3, 则 tanB =【】

已知向量 a, b 满足 |a| = 5, |b| = 6, a · b = −6, 则 cos⟨a, a + b⟩ =【】

在 △ABC 中, cosC = 2/3 , AC = 4, BC = 3, 则 cosB =【】

已知 P 是边长为 2 的正六边形 ABCDEF 内的一点, 则• 的取值范围是【】

在 ① ac =, ② csin A = 3, ③ c = b 这三个条件中任选一个, 补充在下面问题中, 若问题中的三角形存在, 求 c 的值; 若问题中的三角形不存在, 说明理由.问题：是否存在 △ABC, 它的内角 A, B, C 的对边分别为 a, b, c, 且 sinA = sinB, C = π/6 ,__________?注：如果选择多个条件分别解答, 按第一个解答计分.

已知正方形 ABCD 的边长为 2, 点 P 满足 =1/2(+) ,则|| =______ ; · =______ .