双曲线C1: x2/4-y2/b2 =1 与圆 C2 : x2 + y2 = 4 + b2 (b > 0) 交于点 A(xA, yA), 曲线 Γ 满足 x > |xA| 并在曲线 C1、C2 上.
(1) 若 xA=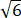 , 求 b 的值;
, 求 b 的值;
(2) b = , 圆 C2 与 x 轴交于点 F1, F2, P 在第一象限, |PF1| = 8, 求 ∠F1PF2;
, 圆 C2 与 x 轴交于点 F1, F2, P 在第一象限, |PF1| = 8, 求 ∠F1PF2;
(3) 点 D(0,b2/2+2), 过该点的直线斜率为 -b/2 的直线 l 和 Γ 只有两个交点, 记作 M, N, 用 b 表示  ∙
∙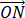 ,并求其取值范围.
,并求其取值范围.
(1) 由于点 A 在 C1, C2 上, 当x_A= 时, 代入曲线方程有 , 且 b > 0, 解得yA= ,b=2. 所以 b 的值为 2.(2) 当 b = 时, 双曲线 C1 方程即x2/4-y2/5=1, 圆 C2 方程即 x2 + y2 = 9.因为 F1, F2 为圆 C2 与 x 轴的左右交点, 所以 F1(−3, 0), F2(3, 0), 恰为双曲线的左右焦点.因为 P 在双曲线 C1 的第一象限图像上, 且 |PF1| = 8, 所以 PF1 − PF2 = 2a = 4, 所以解得 |PF2| = 4.在 △PF1F2 中, |PF1| = 8, |PF2| = 4, |F1F2| = 6, 所以cos∠F1 PF2==(16+64-36)/(2×4×8)=11/16 . 所以,∠F1 PF2=arccos 11/16 .(3) 依题意直线 l 的方程为 y=-b/2 x+2+b2/2 . (先判断直线与曲线 C1 与 C2 的关...
查看完整答案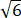 , 求 b 的值;
, 求 b 的值; , 圆 C2 与 x 轴交于点 F1, F2, P 在第一象限, |PF1| = 8, 求 ∠F1PF2;
, 圆 C2 与 x 轴交于点 F1, F2, P 在第一象限, |PF1| = 8, 求 ∠F1PF2; ∙
∙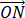 ,并求其取值范围.
,并求其取值范围.
