一圆的中心在直线 5x-3y-7=0 上，且经过两圆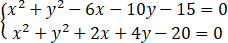
之交点,求此圆的方程式.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
AB 为一圆之一条固定弦，R 是圆上之一运动的点，求三角形 ABR 的垂心的轨迹.
以归纳法证明二项式定理(a+b)n=an+nan-1 b+⋯+n(n-1)⋯(n-r+1)/r! an-r br+⋯+bn
设二圆之连心线交一圆于 A,B 两点，交第二圆于 D,C 二点，又交二圆之一外公切线于 P 点，设在连心线上，点 A 距 P 最近，点 D 距 P 最远，试证：PA· PD = PB·PC.
设 D 为 △ABC 之底边 BC 之中点，若顶角 A 为角直角或锐角，则底边BC 分别大于，等于或小于中线 AD 之二倍.试证之.
若a,b,c为方程式x³+px²+qx+r=0之根，试求以a-1/bc,b-1/ca,c-1/ab为根之方程式.
设圆满足：①截y轴所得弦长为2；②被x轴分成两段圆弧,其弧长的比为3 : 1,在满足条件①②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
设圆过双曲线x2/9 - y2/16=1的一个顶点和-一个焦点，圆心在此双曲线上,则圆心到双曲线中心的距离是________.
直线x + y - 2 = 0截圆x2 + y2 = 4得到的劣弧所对的圆心角为【 】
过原点的直线与圆x2+y2+4x+3=0相切，若切点在第三象限，则该直线的方程是【 】
已知向量=(-1,2),=(3,m)，若⊥，则m=________.
过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是【 】
若向量a=(1,1),b=(1,-1),c=(-1,2)，则c=【 】
设A,B是x轴上的两点，点P的横坐标为2且|PA|=|PB|.若直线PA的方程为x-y+1=0，则直线PB的方程是【 】
已知点P在圆(x-5)2+(y-5)2=16上，点A(4,0)，B(0,2)，则【 】
已知抛物线C:x2=2py(p>0)的焦点为F，且F与圆M:x2+(y+4)2=1上点的距离最小值为4.(1)求p;(2)若P在M上，PA,PB是C的两切线，A,B是切点，求△PAB面积的最大值.
已知圆C:x2+y2=4，直线L:y=kx+m，则当k的值发生变化时，直线被圆C所截的弦长的最小值为1，则m的取值为【 】
已知圆x2+y2-2x-4y=0，则该圆的圆心坐标为__________.
若斜率为√3的直线与y轴交于点A，与圆x2+(y-1)2=1相切与点B，则|AB|=_______.
写出与圆x2+y2=1和(x-3)2+(y-4)2=16都相切的一条直线的方程________________．
设点M在直线2x+y-1=0上，点(3,0)和(0,1)均在⊙M上，则⊙M的方程为______________．
若直线2x+y-1=0是圆(x-a)2+y2=1的一条对称轴，则a=【 】
已知平面直角坐标系中的点集Q={(x,y)|(x-k)2+(y-k2)2=4|k,k∈z}.①存在直线l与Q没有公共点，且Q中存在两点在l的两侧;②存在直线l经过Q中的无数个点则【 】
已知圆C:(x-a)2+(y-2)2=4(a>0)及直线l:x-y+3=0.当直线l被C截得的弦长为2√3时，a=【 】