高中数学-高考试题(印度 2022年反三角函数)

填空题（2022年印度）

计算3/2 cos^-1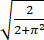+1/4 sin^-1⁡(2√2π)/(2+π² )+tan^-1⁡(√2/π)的值为__________.

答案解析

2.36由常用反三角函数cos-1⁡√(2/(2+π2 ))=tan-1⁡π/√2,sin-1⁡(2√2 π)/(2+π2 )=tan-1⁡(2√2 π)/(π2-2)=tan-1⁡(2∙(√2/π))/(1-(√2/π...

查看完整答案

讨论

高中数学

集合X={x|x是不大于10的正整数}，求满足下列条件的函数f:X→X共有多少个。(1)对于任意不大于9的正整数x，有f(x)≤f(x+1)(2)当1≤x≤5时，f(x)≤x；当6≤x≤10时，f(x)≥x(3)f(6)=f(5)+6.

有6张卡片，正面分别写有数字1~6，背面都写有数字0.起初将这些卡片正面朝上排成一排，且第k个位置上的卡片恰写有数字k.下面利用这6张卡片和一枚均匀的骰子进行如下实验：掷出骰子，若点数为k，则将第k个位置上的卡片翻面，放在原处。进行上述实验3次，若卡片朝上的数字之和为偶数，在这一条件下，骰子恰有一次点数为1的概率为q/p.求p+q的值(p,q为互质整数)

连续型随机变量X的取值范围为0≤X≤a,X的概率密度函数图像如下所示：若P(X≤b)-P(X≥b)=1/4,P(x≤√5)=1/2，则a+b+c的值为【】

某公司生产的洗发水，每瓶容量服从N(m,σ²)的正态分布。随机抽取16瓶，用样本均值推断m的95%置信区间为746.1≤m≤755.9.若随机抽取n瓶，用样本均值推断m的99%置信区间为a≤m≤6.已知P{|Z|≤1.96}=0.95，P{|Z|≤2.58)=0.99，要使b-a不大于6，n最小为【】

袋中装有1个写有数字1的白球、1个写有数字2的白球、1个写有数字1的黑球和3个写有数字2的黑球。一次性从袋中随机取出3个球，记“取出的是1个白球、2个黑球”为事件A，“3个球上数字的乘积为8”为事件B，则P(A∪B)为【】

盒子中装有5个白色口罩和9个黑色口罩.一次性从盒中随机抽取3个口罩，至少有一个白色口罩的概率是【】

从数字1，2，3，4，5可重复地选出4个，能排列成多少个大于4000的奇数【】

在(x3+3)5的展开式中，x9项的系数为【】

最高次项系数为1的三次函数f(x)和实数集上的连续函数g(x)满足下列条件，求f(4).(1)对于任意实数x,f(x)=f(1)+(x-1) f' [g(x)],(2)函数g(x)的最小值为5/2,(3) f(0)=-3,f[g(1)]=6.

对于正整数n，函数f(x)定义如下：f(x)=对于实数t，记方程f(x)=t的不同实数解的数量为g(t)，求使得函数g(t)的最大值为4的所有正整数n的和.

反三角函数

若0<α<1，在[0,2π]上满足sinx≥α的x的范围是【】

函数y=arccos⁡(sinx)(- π/3<x<2π/3)的值域是【】

使arcsinx>arccosx成立的x的取值范围是【】

若0<α<π/2，则acrsin⁡[cos⁡(π/2+a) ]+arccos⁡[sin⁡(π+α) ]等于【】

满足arccos⁡(1-x)≥arccos的x的取值范围是【】

函数y=cos⁡x+1(-π≤x≤0)的反函数是【】

设x=sinα,且α∈[-π/6,5π/6]，则arccos⁡x的取值范围是________.

求sin⁡(2arcsin(⁡4/5))的值.

函数f(x)=sinx,x∈[π/2,3π/2]的反函数f-1(x)=【】

tan(arctan1/5+arctan3)的值等于【】

三角函数

已知sin2(π/4+α)=2/3, 则sin2α的值是_______.

将函数y=3sin⁡(2x+π/4)的图象向右平移 π/6 个单位长度, 则平移后的图像中与 y 轴最近的对称轴的方程是__________.

全国统考三角函数的诱导公式

已知0<x<π/2，简化： lg⁡(cos⁡x•tan⁡x+1-2sin2⁡(x/2))+lg⁡[cos⁡( x-π/4)]-lg⁡( 1+sin⁡2 x).

函数y=sin2xcos2x是【】

要得到函数y=sin(2x-π/3)的图像，只需将函数y=sin2x的图像（如图）【】

函数y=arccos⁡(cosx)(x∈[-π/2,π/2])的图像是【】

如果|cosθ|=1/5,5π/2<θ<3π，那么sin(θ/2)的值等于【】

如图是函数y=2sin(ωx+φ)(|φ|<π/2)的图像，那么【】

设函数y=arctanx的图像沿x轴正方向平移两个单位所得到的图像为C.又设C'与C关于原点对称，那么C'所对应的图像是【】