高中数学-高考试题(河南省 1977年四边形)

证明题（1977年河南省）

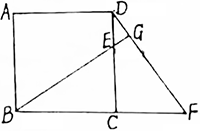
如图，已知正方形ABCD的边CD上任意一点E.延长BC到F，使CF=CD.设BE与DF相交于G，求证：BG⊥DF.

答案解析

暂无答案

讨论

四边形

⊙O 的半径是 a，ABCD 是它的内接四边形，∠A =75°，∠B = 120°，AB = BC，求四边形各边长.

梯形之四边长均为已知，求作此梯形.

于四边形之内，取一点不在两对角线之交点之上者，试证明从此点至各顶点之距离之和大于两对角线之和.

试作一正方形，与一已知长方形之面积相等.

设有一三角形，其底为 7 cm，高为 5 cm，用圆规及尺作一正方形,其面积与此相等者.

Show that the line joining the mid-points of the diagonals of a trapezoid is half the difference of its bases.

Transform the difference of two squares into a rectangle, the ratio of two sides being 2 : 3.

PQRS为平面四边形，QR=1，∠PQR= ∠QRS= 70°，∠PQS=15°，∠PRS= 40°.若∠RPS=θ.PQ=α,PS=β，则4αβsinθ属于下列哪个区间【】

求作一四角形，与一已知四角形等角而外切于一定圆.

设ABCD为一平行四边形，AC为对角线，由B作任意直线各交AC、CD及AD于F、G及E，求证EF·FG=BF².

三角形

证明 △ABC 中过 B,C 二顶点之二中线等长，则 △ABC 为等腰，并证明其逆定理.

With BC, one leg of △ABC, as diameter, a circle is described intersecting the hypotenuse AC at P. From P draw a tangent intersecting AB at D. Showt hat AD = BD.

The sides of a triangle are 149,163 and 222. To find(1) The area of the triangle.(2) The radius of the inscribed circle.(3) The angles of the triangle.

在△ABC的边AB,AC上各取D,E点，使AD=1/3 AB,AE=1/3 AC，连结BE,CD相交于F点.求证：S△FBC=1/2 S△ABC.

设 △ABC 的重心为 G，BC、CA 的中点为 E、F，设 △ABC 的面积为 K，求△GEF 的面积.

在锐角三角形ABC中，AB<AC.设Ω为三角形ABC的外接圆.点S是Ω上包含点A的弧BC的中点.过点A作垂直于BC的直线与BS交于点D,与圆Ω交于另一点E,E≠A.过点D且平行于BC 的直线与直线BE交于点L.记ω为三角形BDL的外接圆.设ω与Ω交于另一点P,P≠B.证明：ω在点P处的切线与直线BS的交点在∠BAC的内角平分线上.

Consider the convex quadrilateral ABCD. The point P is in the interior of ABCD. The following ratio equalities hod:∠PAD:∠PBA:∠DPA=1:2:3=∠CBP:∠BAP:∠BPC.Prove that the following three lines meet in a point : the internal bisectors of angles ∠ADP and ∠PCB and the perpendicular bisector of segment AB.设P是凸四边形ABCD内部一点，且满足：∠PAD:∠PBA:∠DPA=1:2:3=∠CBP:∠BAP:∠BPC.证明：∠ADP的内角平分线、∠PCB的内角平分线和线段AB的中垂线，三线共点。（波兰供题）

已知△ABC三内角的大小成等差数列，tanAtanC=2+，求角A，B，C的大小；又知顶点C的对边c上的高等于4，求三角形各边a，b，c的长.（提示：必要时可验证(1+)2=4+2）

直角三角形之斜边上所画之正三角形之面积，等于其余两边上所画之正三角形之面积之和.

试言已知三角形之两角及一角之对边,求作其形之方法.

平面几何

作直线垂直于一已知线，与已知圆相切.

从半圆之直径 AB 两端各引此半圆弦 AC,BD交于 E，求证: AC·AE+BD·BE = AB².

两圆外切，其半径各为R和r，设两圆之外公切线之交角为θ，试证 sinθ=.

于圆内接四边形内，若两对角线成垂直，求证对角线交点与一边中点之距离等于自圆心至对边之距离.

某城街路为棋盘式，走向南北者有 a 条，而走向东西者有 6 条，一行人欲由西北隅向最短之路走到东南隅，问计共有若干方法？

A,B,C 为三定点，求作一圆过 A,B，使从 C 到此圆的切线等于定长.

已知PA,PB,PC为过圆周上点P三弦，PT为圆之切线，设有一直线与PT平行，交PA,PB,PC于A',B',C'三点.求证：PA∙PA'=PB∙PB'=PC∙PC'.

两圆面积比等于它们的半径比.

设 △ABC 是一个圆的内接三角形，过 A 作切线交于 BC 的延长线于 D.证明 △ABD,△ACD 的外接圆直径的比等于 AD:CD.

自 △ABC 的顶点 A 至对边作垂线，自垂足 D 作 AB、AC 过之垂线，其垂足为 E、F，证明 B,E,F,C 共圆.