初中数学-中考试题(河北省 2022年全等)

问答题（2022年河北省）

如图，四边形ABCD中，AD//BC,∠ABC=90°,∠C=30°,AD=3,AB=2√3,DH⊥BC于点H,将△PQM与该四边形按如图方式放在同一平面内，使点P与A重合，点B在PM上，其中∠Q=90°,∠QPM=30°,PM=4√3.

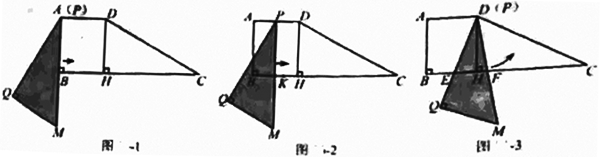
(1)求证：△PQM≅△CHD;

(2) △PQM从图1的位置出发，先沿着BC方向向右平移(图2)，当点P到达点D后立刻绕点D逆时针旋转(图3)，当边PM旋转50°时停止.

①边PQ从平移开始，到绕点D旋转结束，求边PQ扫过的面积;

②如图2点K在BH上，且BK=9-4√3.若△PQM右移的速度为每秒1个单位长，绕点D旅转的速度为每秒5°，求点K在△PQM区域(含边界)内的时长;

③如图3在△PQM旋转过程中，设PQ,PM分别交BC于点E,F，若BE=d，直接写出CF的长(用含d的式子表示).

答案解析

(1)∵AD//BC,DH⊥BC∴DH⊥AD则在四边形ABHD中，∠ABH=∠BHD=∠HDA=90°,故四边形ABHD为矩形，∴DH=AB=2√3,BH=AD=3.在Rt△DHC中，∠C=30°∴CD=2DH=4√3,CH=√3 DH=6.∵∠DHC=∠Q=90°,∠C=∠QPM=30°,CD=PM=4√3∴△PQM≅△CHD(AAS)(2)①过点Q作QS⊥AM于S由(1)得AQ=CH=6在Rt△AQS中，∠QAS=30°∴AS=√3/2 AQ=3√3.平移扫过的面积：S1=AD∙AS=3×3√3=9√3旋转扫过的面积：S2=(50°)/(360°)∙π∙PQ2=(50°)/(360°)∙π∙62=5π故边PQ扫过的面积：S=S1+S2=9√3+π.②运动分两个阶段：平移和旋转.平移阶段：KH=BH-BK=3-(9-4√3)=4√3-6∴t1=KH/v=(4√3-6)s旋转阶段：PM=2DM取刚开始旋转状态，以PM为直径作圆，则H为圆心，延长DK与圆相交于点G，连接GH,GM，过点G作GT⊥DM于T,设∠KDH=θ，则∠GHM=2θ在Rt△DKH中：KH=BH-BK=4√3-6=2√3(2-√3) DK===4√3× 设t= ，则KH=2√3 t2,DK=4√...

查看完整答案

讨论

旋转

如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，则下列四个图形中正确的是【】

如图，在边长为6的正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，将ΔADF绕点A顺时针旋转90°得到ΔABG.若DF=3，则BE的长为__________.

如图的四个三角形中，不能由△ABC经过旋转或平移得到的是【】

在△ABC中，∠ACB＝90°，CD是中线，AC＝BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E、F，DF与AC交于点M，DE与BC交于点N．（1）如图1，若CE＝CF，求证：DE＝DF；（2）如图2，在∠EDF绕点D旋转的过程中，试证明CD2＝CE•CF恒成立；（3）若CD＝2，CF＝，求DN的长．

如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在某个点上，在建立平面直角坐标系后，点A的坐标为(-6，1)，点B的坐标为(-3，1)点C的坐标为(-3，3).(1)将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1，试在图上画出的图形Rt△A1B1C1，并写出点A1的坐标；(2)将原来的R△ABC绕点B顺时针旋转90°得到Rt△A2B2C2，试在图上画出Rt△A2B2C2的图形.

如图，在△ABC中，AB=AC，若M是BC边上任意一点，将△ABM绕A逆时针旋转得到△ACN，点M的对应点为点N，连接MN，则下列结论一定正确的是【】

将一个矩形纸片OABC放置在平面直角坐标系中，点O(0,0),A(3,0),C(0,6)，点P在边OC上(点P不与点O,C重合)，折叠该纸片，使折痕所在的直线经过点P，并与x轴的正半轴相交于点Q,且∠OPQ=30°，点O的对应点O'落在第一象限.设OQ=t. (I)如图①，当t=1时，求∠O'QA的大小和点O'的坐标:(Ⅱ)如图②，若折叠后重合部分为四边形，O' Q,O'P分别与边AB相交于点E,F，试用含有t的式子表示O'E的长，并直接写出t的取值范围:(Ⅲ)若折叠后重合部分的面积为3√3，则t的值可以是__________(请直接写出两个不同的值即可).

如图，将ΔABC先向右平移3个单位，再绕原点O旋转180°得到ΔA'B'C'，则点A的对应点A'的坐标是【】

如图，在Rt△ABC中，∠ACB=90°,AB=5cm,BC=3cm，将△ABC绕点A按逆时针方向旋转90°得到△ADE，连接CD.点P从点B出发，沿BA方向匀速运动,速度为1cm/s，同时，点Q从点A出发，沿AD方向匀速运动，速度为1m/s. PQ交AC于点F，连接CP,EQ，设运动时间为t(s)(0<t<5).解答下列问题：(1)当EQ⊥AD时，求t的值;(2)设四边形PCDQ的面积为S(cm^2)，求S与t之间的函数关系式;(3)是否存在某一时刻t，使PQ//CD?若存在，求出t的值；若不存在，请说明理由.

如图，在正方形ABCD中，AB=3，点E，F分别在边AB，CD上，∠EFD=60°.若将四边形EBCF沿EF折叠，点B恰好落在AD边上，则BE的长度为【】

全等

如图，四边形ABCD是菱形，点E，F分别在BC，DC边上，添加以下条件不能判定△ABE≌△ADF的是【】

如图，在△ABC中，AB=AC,∠BAC=α,M为BC的中点，点D在MC上，以点A为中心，将线段AD顺时针旋转α得到AE，连接BE,DE.(1)比较∠BAE与∠CAD的大小；用等式表示线段BE,BM,MD之间的数量关系，并证明；(2)过点M作AB的垂线，交DE于点N,用等式表示线段NE与ND的数量关系，并证明.

如图，△ABC和△DEF中，AB=DE，∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF【】

如图，点M，N分别在正方形ABCD的边BC，CD上，且∠MAN=45°.把ΔADN绕点A顺时针旋转90°得到ΔABE. （1）求证：ΔAEM≌ΔANM.（2）若BM=3，DN=2，求正方形ABCD的边长.

已知：如图，E、F在AC上，AD//CB且AD=CB，∠D=∠B.求证：AE=CF.

如图所示、△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.(1)求证:△AOC≌△BOD;(2)若AD=1,BD=2,求CD的长.

如图，AC与BD交于点O，OA=OD，∠ABO=∠DCO，E为BC延长线上一点，过点E作EF//CD，交BD的延长线于点F.(1)求证△AOB≌△DOC;(2)若AB=2,BC=3,CE=1，求EF的长.

如图，在四边形ABCD中，AD=BC,AC=BD,AC与BD相交于点E.求证：∠DAC=∠CBD.

如图，点E、F在线段BC上，AB//CD，∠A=∠D,BE=CF，证明：AE=DF.

在△ABC中，∠ACB=90°，D为△ABC内一点，连接BD，DC延长DC到点E，使得CE=DC. (1)如图(左)，延长BC到点F，使得CF=BC，连接AF、EF，若AF⊥EF，求证：BD⊥AF.(2)连接AE，交BD的延长线干点H，连接CH，依题意补全图(右)，若AB²=AE²+BD²，用等式表示线段CD与CH的数量关系，并证明.

三角形

如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE．若BC＝6，AC＝5，则△ACE的周长为【】

已知三角形两边的长分别是4和10，则此三角形第三边的长可能是【】

如图,在△ABC中,AB=AC,∠ABC=72°.(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.

如图,小山岗的斜坡AC的坡度是tanα=3/4,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26:6°=0.45, cos26.6°=0.89, tan26.6°=0.50).

如图，△ABC的内心在y轴上，点C的坐标为(2，0)，点B的坐标是(0，2)，直线AC的解析式为y=1/2 x-1，则tanA的值是______.

如图，在平面直角坐标系中，△AOB的边AO、AB的中点C、D的横坐标分别是1、4，则点B的横坐标是______.

如图，已知点O是△ABC的外心，∠A=40°，连结BO、CO则∠BOC的度数是【】

如图，在△ABC中，点D、E分别是BC、AC的中点，AD与BE相交于点F，若BF=6，则BE的长是________.

我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为a,b,c，记p=(a+b+c)/2，则其面积S=.这个公式也被称为海伦-秦九韶公式.若p=5,c=4，则此三角形面积的最大值为【】

如图，等腰直角三角形ABC中，∠A=90°，BC=4.分别以点B、点C为圆心，线段BC长的一半为半径作圆弧，交AB、BC、AC于点D、E、F，则图中阴影部分的面积为________.