如图,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN=45°.把ΔADN绕点A顺时针旋转90°得到ΔABE.
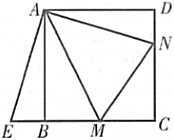
(1)求证:ΔAEM≌ΔANM.
(2)若BM=3,DN=2,求正方形ABCD的边长.
如图,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN=45°.把ΔADN绕点A顺时针旋转90°得到ΔABE.

(1)求证:ΔAEM≌ΔANM.
(2)若BM=3,DN=2,求正方形ABCD的边长.
证明:(1)如图,由旋转知ΔADN≌ΔABE,∴AN=AE,∠1=∠2.∵∠BAD=90°,∠MAN=45°,∴∠1+∠3=45°,∴∠2+∠3=45°.∴∠EAM=∠NAM=45°.在ΔAEM和ΔANM中,,∴ΔAEM≌ΔANM. 解:(2)由(1)知ME=MN,即BM...
查看完整答案如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF【 】
已知:如图,E、F在AC上,AD//CB且AD=CB,∠D=∠B.求证:AE=CF.
如图,在四边形ABCD中,AD=BC,AC=BD,AC与BD相交于点E.求证:∠DAC=∠CBD.
如图,点E、F在线段BC上,AB//CD,∠A=∠D,BE=CF,证明:AE=DF.
如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是【 】
如图所示、△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.(1)求证:△AOC≌△BOD;(2)若AD=1,BD=2,求CD的长.
如图,在△ABC中,AD平分∠BAC,DE⊥AB,若AC=2,DE=1,则S△ACD=________.
已知点O是边长为6的等边△ABC的中心,点P在△ABC外,△ABC,△PAB,△PBC,△PCA 的面积分别记为S0,S1,S2,S3.若S1+S2+S3=S0,则线段OP长的最小值是【 】
如图,有一张一个角为 30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是【 】
小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为 60°,求山高【 】
已知BD 垂直平分AC,∠BCD=∠ADF,AF⊥AC.(1)证明四边形ABDF是平行四边形;(2)若AF=DF=5,AD=6,求AC的长.
如图,已知△ABC,AB<BC,用尺规作图的方法在BC 上取一点P,使得PA+PC=BC,则下列选项正确的是【 】
如图,在△ABC中,AB=AC,∠ABC=72°.(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.