在△ABC中，∠ACB=90°，D为△ABC内一点，连接BD，DC延长DC到点E，使得CE=DC.
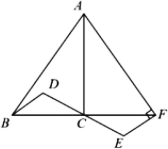
(1)如图(左)，延长BC到点F，使得CF=BC，连接AF、EF，若AF⊥EF，求证：BD⊥AF.
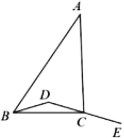
(2)连接AE，交BD的延长线干点H，连接CH，依题意补全图(右)，若AB²=AE²+BD²，用等式表示线段CD与CH的数量关系，并证明.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
关注优题吧，注册平台账号.
在△ABC中，∠ACB=90°，D为△ABC内一点，连接BD，DC延长DC到点E，使得CE=DC.
(1)如图(左)，延长BC到点F，使得CF=BC，连接AF、EF，若AF⊥EF，求证：BD⊥AF.
(2)连接AE，交BD的延长线干点H，连接CH，依题意补全图(右)，若AB²=AE²+BD²，用等式表示线段CD与CH的数量关系，并证明.
(1)在△FCE和△BCD中， CE=CD，∠FCE=∠BCD，CF=CB∴△FCE≌△BCD(SAS)∴∠CFE=∠CBD，∴EF// BD，∵AF⊥EF,∴BD⊥AF.(2)解:补全后的图形如图所示，CD=CH，证明如下:延长BC到点M，使CM=CB，连接EM，AM,∵∠ACB=90°，CM=CB,∴AC垂直平分BM，∴AB=AM，在△...
查看完整答案