设函数f(x)连续可导,且f(0)=1,0<f'(x)<1/2.设{xn}满足:xn+1=f(n),(n=1,2,⋯),证明:
(1)级数 (xn+1-xn)绝对收敛.
(xn+1-xn)绝对收敛.
(2)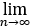 xn存在,且0<
xn存在,且0<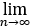 xn <2.
xn <2.
设函数f(x)连续可导,且f(0)=1,0<f'(x)<1/2.设{xn}满足:xn+1=f(n),(n=1,2,⋯),证明:
(1)级数 (xn+1-xn)绝对收敛.
(xn+1-xn)绝对收敛.
(2)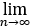 xn存在,且0<
xn存在,且0<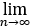 xn <2.
xn <2.
解答过程见word版
设函数f(x)在区间[0,+∞)上可微,且满足条件:0≤f(x)≤x/(1+x²)(0≤x<+∞)求证:存在ξ>0,使得f'(ξ)=(1-ξ²)/(1+ξ²)².
证明:函数项级数(-1)n/(x²+n)在区间x∈(-∞,+∞)上一致收敛.
讨论:当α>0时,函数f(x)=xα在区间[0,+∞)上的一致连续性.
设有界区域Ω由平面2x+y+2z=2与三个坐标平面围成,Σ为Ω整个表面的外侧,计算曲面积分:I=∬Σ(x²+1)dydz-2ydzdx+3zdxdy
已知L是第一象限中点从点(0,0)沿圆周x²+y²-2x=0到点(2,0),再沿圆周x²+y²=4到点(0,2)的曲线段,计算I=∫L3x²ydydx+(x³+x-2y)dy
求圆锥体z≥与球体x²+y²+(z-1)²≤1所围立体的体积.
设级数an 绝对收敛,bn 收敛,且an =A,bn =B,令cn=a1bn+a2bn-1+⋯+an b1=akbn-k+1,则cn =AB.
设f(n)=a0+ak/nk ,且满足|a_k |≤M,这里n,k均为正整数,试证:数项级数f(n)收敛的充要条件为a0=a1=0.
设级数sinnx/(1+nx2)(1)当x取何值时,级数绝对收敛?并说明理由;(2)当x取何值时,级数条件收敛?并说明理由.
已知an<bn (n=1,2,⋯), 若级数an ,与bn 均收敛,则“an 绝对收敛”是“bn 绝对收敛的”【 】
若un>0,n=1,2,…且∀n,un+1/un <1则un 收敛.
已知a1=2,an+1=1/2 (an+1/an ),证明:(1)数列{an }收敛;(2) (an/an+1 -1) 收敛.