设矩阵A=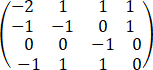
，则A的最小多项式为__________.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设A=(aij)为2阶复方阵，满足tr(Ak)=k(k=1,2)，其中tr(A)=a11+a22为矩阵A的迹，则行列式|A|=______.
设A=,B=,C=若矩阵满足AXB=C，则X=________.
计算Gauss曲面积分I=∬Scos((n,r) ̂)/r² dS，其中S为光滑封闭曲面，原点不在S上，r为S上动点至原点的距离，(n,r) ̂为动点处外法向量n与径向r的夹角.
设f(n)=a0+ak/nk ，且满足|a_k |≤M，这里n,k均为正整数，试证：数项级数f(n)收敛的充要条件为a0=a1=0.
设函数f(x)在I上有定义，令ωf(δ)=|f(x)-f(y)|证明：(1)ωf(δ)存在.(2) f(x)在区间I上一致连续等价于ωf(δ)=0.
设数列{xn}有界，且(xn+1-xn)=0，令 m=xn ,M=xn,m<M证明：在区间(m,M)上任意一个数都是此数列的一个子列的极限.
设A为3阶矩阵，A*为A的伴随矩阵，E为3阶单位矩阵.若r(2E-A)=1,r(E+A)=2，则|A* |=______.
设n阶矩阵A 的各行素之和均为3，E为单位阵则阵A²-2A +E的各行元素之和为______.
设A(λ),B(λ)都是数域P上m×n的λ矩阵，则A(λ),B(λ)等价的充要条件为A(λ)与B(λ)有相同的初等因子组.
设A是2022阶可逆对称实方阵，则A必有2021阶非零主子式
设A = aij为3阶矩阵，Aij为代数余子式，若A的每行元素之和均为2，且|A| = 3，A11 + A21 + A31 = ______.
设A=,A*为A的伴随矩阵，则|(1/4 A)-1 - 15A* |=________.
设矩阵A=,β=，已知线性方程组AX=β有解但不唯一.(1)求a的值；(2)求一个正交矩阵Q，使得QTAQ为对角矩阵.
设二次型f(x1,x2 )=x1²-4x1 x2+4x2²经正交变换=Q化为二次型g(y1,y2 )=ay1²+4y1 y2+by2²，其中a≥b.(1)求a,b的值；(2)求正交矩阵Q.
设A为2阶矩阵，P(α,Aα)，其中α是非零向量且不是A的特征向量(1)证明P为可逆矩阵；(2)若A²α+Aα-6α=0，求P-1AP，并判断A是否相似于对角矩阵.
证明：秩等于r的矩阵可以表示为r个秩等于1的矩阵之和，但不能表示为少于r个秩等于1的矩阵之和.
设A是n阶满秩矩阵，证明：存在正交矩阵P1,P2使得P1-1AP2=其中λi>0(i=1,2,⋯,n).
设A为4阶矩阵，A*为A的伴随矩阵，若A(A-A*)=0，且A≠A*，则r(A)取值为【 】