证明方程lnx=x/e-
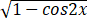dx在区间(0,+∞)内有且仅有两个不同实根.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
证明题（1989年理工数学Ⅰ；1989年理工数学Ⅱ）
答案解析
因为dx=√2 sinxdx=2√2，原方程相当于lnx=x/e-2√2.令F(x)=x/e-2√2-lnx，则F' (x)=1/e-1/x，令F' (x)=0得x=e.当0<x<e时，F' (x)<0,F(x)严格单调减少；当e<x<+∞时，F' (x)>0,F(x)严格单调增加...
查看完整答案讨论
设实系数一元n次方程P(x)=a0xn+a1xn-1+…+an-1x+an (a0≠0，n≥2)的根全为实数，证明：方程P′(x)=0的根也全为实数.
若函数f(x)在[a,b]上连续(b>0)，在(a,b)内可导，且f(a)=0，证明：存在ξ∈(a,b)，使得f'(ξ)=ξf(ξ)/(b-ξ).
设f在[0,1]上连续，在(0,1)上有二阶连续导数，f(0)=f(1)=1,f'' (x)<8，证明：对任意的x∈[0,1]，有f(x)>0.
设f(x)在[0,+∞)上连续可导，f(0)=1，且对一切x≥0有|f(x)|≤e-x，求证：∃ξ∈(0,+∞)，使得f'(ξ)=e-ξ .
已知f(x)在[a,b]上三次可微，且f(a)=f' (a)=f(b)=0,|f''' (x)|≤M,证明：|f(x) dx|≤M/72 (b-a)4.
设f(x)在(0,1)上可导，在[0,1]上连续，且f(1)-f(0)=2e-1-1.证明：存在ξ∈(0,1)，使得eξ^2 f' (ξ)+2ξ3=0.
设函数f(x)在[0,1]上二阶可导，且f(0)=0，f(1)=1，求证：存在ξ∈(0,1)，使得ξf″(ξ)+(1+ξ)f’(ξ)=1+ξ.
设函数f(x)在(-∞,+∞)上具有二阶导数，并且f″(x)>0，f′(x)=α>0，f′(x)=β<0，且存在一点x0使得f(x0)<0，证明：方程f(x)=0在(-∞,+∞)上恰有两个实根.
求函数f(x)=x2/(1+x2 )的极值与拐点，并求拐点处的切线方程.
设函数f(x)在开区间(a,b)内存在二阶导数f''(x)，且在(a,b)内f''(x)>0，证明：对于任意两点x1,x2∈(a,b)，恒有f((x1+x2)/2)≤(f(x1)+f(x2))/2.
曲线y=arctanx在横坐标为1的点处的切线方程是__________；法线方程是____________.
已知f(x)在[a,b]上二阶可导，且f''(x)≤0，证明：f(x)dx≤(b-a)f((a+b)/2).
设函数f(x)在(0,+∞)上连续可导，f(x)存在，f(x)的图形在(0,+∞)是上凸的，求证：f′(x)=0.
当x→0时，x-sinxcosxcos2x与cx4为等价无穷小，则c=__________，k=__________.
当x→0时，1-cosxcos2xcos3x对于无穷小x的阶数等于 __________.
设x0,x1,…,xn为n+1个互异的插值节点，li (x)(i=0,1,…,n)为拉格朗日基本插值多项式（也称为插值基本函数）。证明：(1) li (x)≡1;(2) li (x)xik≡xk.
设f(x)=nx(1-x)n（n为自然数），求(1) f(x)在[0,1]上的最大值M(n)={f(x)}.(2)求M(n).