在边长为1的正方形ABCD中,E为CD的三等分点,CE=1/2 DE,BE=λBA+μBC,则λ+μ=______;若F为线段BE上的动点,G为AF的中点,则AF∙DG的最小值为______.
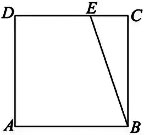
在边长为1的正方形ABCD中,E为CD的三等分点,CE=1/2 DE,BE=λBA+μBC,则λ+μ=______;若F为线段BE上的动点,G为AF的中点,则AF∙DG的最小值为______.

①4/3;②-5/18.
【解析】
解答过程见word版
设有A,B,C,D,E五种活动,甲、乙都要选择三个活动参加.(1)甲选到A的概率为______;(2)已知乙选了A活动,他再选择B活动的概率为______.
已知(x-1)²+y²=25的圆心与抛物线y²=2px(p>0)的焦点重合,A为两曲线的交点,则原点到直线AF的距离为______.
在(3/x³ +x³/3)6的展开式中,常数项为______.
已知i是虚数单位,复数(√5+i)⋅(√5-2i)=________.
一个五面体ABC-DEF,已知AD∥BE∥CF,且两两之间距离为1,并已知AD=1,BE=2,CF=3,则该五面体的体积为【 】
已知双曲线x²/a² -y²/b² =1(a>0,b>0)的左右焦点分别为F1,F2,P是双曲线右支上一点,且直线PF2的斜率为2,△PF1 F2是面积为8的直角三角形,则双曲线的方程为【 】
已知函数f(x)=sin3(ωx+π/3)(ω>0)的最小正周期为π,则f(x)在区间[-π/12,π/6]上的最小值是【 】
设m,n为两条不同的直线,α为一个平面,则下列结论正确的是【 】
已知向量a,b满足|a|=1,|a+2b|=2,且(b-2a)⊥b,则|b|=【 】
已知k∈R,a=(2,5),b=(6,k),且a∥b ,则k的值为________.
已知单位向量 a, b 的夹角为 60°, 则下列向量中, 与 b 垂直的是【 】
已知 P 是边长为 2 的正六边形 ABCDEF 内的一点, 则• 的取值范围是【 】
已知正方形 ABCD 的边长为 2, 点 P 满足 =1/2(+) ,则|| =______ ; · =______ .
已知单位向量 e1, e2 满足|e1-e2 |≤, 设 a = e1 + e2, b = 3e1 + e2, 向量 a, b 的夹角为 θ, 则 cos2θ的最小值为_______.
已知曲线C:x²+y²=16(y>0),从C上任意一点P向x轴作垂线段PP',P'为垂足,则线段PP'的中点M的轨迹方程为【 】
抛物线C:y²=4x的准线为l,P为C上的动点,过P作⨀A:x²+(y-4)²=1的一条切线,Q为切点,过P作l的垂线,垂足为B,则【 】
记△ABC的内角A,B,C对应的边分别为a,b,c,已知sinA+√3 cosA=2.(1)求A.(2)若a=2,√2 bsinC=csin2B,求△ABC的周长.
在平面直角坐标系xOy中,椭圆x²/a² +y²/b² =1(a>b>1)的右焦点为F(c,0),若存在经过焦点F的一条直线l交椭圆于A,B两点,使得OA⊥OB.求椭圆的离心率e=c/a的取值范围.
已知双曲线的两个焦点分别为(0,4),(0,-4),点(-6,4)在该双曲线上,则该双曲线的离心率为【 】
记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b²=9/4 ac,则sinA+sinC=【 】
已知b是a,c的等差中项,直线ax+by+c=0与圆x²+y²+4y-1=0交于A,B两点,则|AB|的最小值为【 】