已知集合所以A={x│5x-a≤0},B={x│6x-b>0},a,b∈N，且A∩B∩N={2,3,4}，则整数对(a,b)的个数为【 】.
A、20
B、25
C、30
D、42
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
单项选择（2006年全国高中数学联赛）
答案解析
C
【解析】
由5x-a≤0得x≤a/5，由6x-b>0得x>b/6.
要使A∩B∩N={2,3,4}，则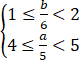
即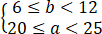
，
所以数对(a,b)共有C61 C51=30个.
讨论
已知集合A和集合B各含有12个元素，A∩B含有4个元素，试求同时满足下面两个条件的集合C的个数：(Ⅰ) C ⊂ A∪B，且C中含有3个元素；(Ⅱ) C∩A≠∅(∅表示空集).
假设在200件产品中有3件是次品，现在从中任意抽取5件，其中至少有2件次品的抽法有【 】种.
由数字1，2，3，4，5组成的没有重复数字的五位数，其中小于50000的偶数共有【 】个
平面上，四条平行直线与另外五条平行直线互相垂直，则它们构成的矩形共有______个（结果用数值表示）.
已知甲、乙两组各有8人，现从每组抽取4人进行计算机知识竞赛，比赛人员的组成共有__________种可能（用数字作答）.
某学校开设了4门体育类选修课和4门艺术类选修课, 学生需从这8门课中选修2门或3门课, 并且每类选修课至少选修1门, 则不同的选课方案共有 ______种(用数字作答).
4 名同学到 3 个小区参加垃圾分类宣传活动, 每名同学只去 1 个小区, 每个小区至少安排 1 名学生, 则不同的安排方法有______种
6 名同学到甲、乙、丙三个场馆做志愿者, 每名同学只去 1 个场馆, 甲场馆安排 1 名, 乙场馆安排 2 名, 丙场馆安排 3 名, 则不同的安排方法共有【 】
设集合A={x│x≥1},B={x|-1<x<2}，则A∩B=【 】
已知集合 U = {−2, −1, 0, 1, 2, 3}, A = {−1, 0, 1}, B = {1, 2}, 则 CU (A ∪ B) =【 】
某中学的学生积极参加体育锻炼, 其中有 96% 的学生喜欢足球或游泳, 60% 的学生喜欢足球, 82% 的学生喜欢游泳, 则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是【 】
数值X={(2n+1)π,n是整数}与数集Y={(4k±1)π,k是整数}之间的关系是【 】。
如果I={a,b,c,d,e},M={a,c,d},N={b,d,e}，其中I是全集，那么M ̅∩N ̅等于【 】
设全集I={(x,y)|x,y∈R}，集合M={(x,y)│(y-3)/(x-2)=1},N={(x,y)|y≠x+1}，那么等于【 】
设全集为R,f(x)=sinx,g(x)=cosx,M={x│f(x)≠0},N={x|g(x)≠0}，那么集合{x|f(x)g(x)=0}等于【 】
设集合A={x|2lgx=lg(8x-15),x∈R},B={x|cos(x/2)>0,x∈R}，则A∩B的元素个数为______.
已知A={x│2x≤1},B={-1,0,1}，则A∩B=__________.
已知集合M={-2,-1,0,1,2},N={x|x²-x-6≥0}，则M∩N=【 】
已知 A = {1, 2, 4}, B = {2, 4, 5}, 则 A ∩ B =__________.
已知集合 P = {x | 1 < x < 4}, Q = {x | 2 < x < 3}, 则 P ∩ Q =【 】
已知集合 A = {−1, 0, 1, 2}, B = {0, 2, 3}, 则 A ∩ B =__________.
已知集合E={θ|cosθ<sinθ,0≤θ≤2π},F={θ|tanθ<sinθ}，那么E∩F的区间为【 】