在图中的几何体是由棱长为 1 厘米的小正方体拼搭成的,它的表面积是______平方厘米,至少还需要______个这样的小正方体,才能拼搭成棱长为 3 厘米的一个正方体。
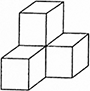
在图中的几何体是由棱长为 1 厘米的小正方体拼搭成的,它的表面积是______平方厘米,至少还需要______个这样的小正方体,才能拼搭成棱长为 3 厘米的一个正方体。

18 23
定义新运算:已知1※3 = 1×2×3 , 4 ※ 5 = 4×5×6×7×8 ,则(6※4)÷ (3※4)=__________。
一根竹竿, 小明从左端量到 3 米处做一个记号 A ,再从右端量到 3 米处做一个记号 B 。这时,他发现 A , B 之间的长度恰好是全长的 20 % ,这根竹竿的长度可能是多少米?
某班有学生56人,抽出男生人数的1/4与女生人数的1/5后,还剩43人,这个班有男、女生各多少人?
修一条路,第一天修了全长的一半多 6 米,第二天修了余下的一半少 20 米,第三天修了 30 米,最后还刹 14 米没修。这条路长多少米?
在一只底面直径是 60 厘米的圆柱形水捅里,有一段半径为 10 厘米的圆柱形钢材浸没在水中,当钢材从储水捅里被取出时,桶里的水面下降了 5 厘米,这段钢材有多长?
甲船逆水航行 360 千米需要 18 小时,返回原地需要 10 小时。乙般逆水航行同样一段距离需要15小时,返回原地需要多少小时?
有边长1米的正方体2100个,堆成了一个实心的长方体。它的高是10米,长、宽都大于高。问长方体的长与宽的和是几米?
如图,将圆柱形玻璃杯的水倒入下面编号为【 】号圆锥形容器里,正好倒满(单位:厘米)
一个棱长为a米的正方体,任意截成两个长方体,则两个长方体的表面积之和是【 】a2平方米。
用一根长24分米的铁丝做一个长方体框架,使它的长、宽、高的 比是5:4:3。这个长方体的体积是【 】立方分米。
一个圆柱和圆锥等底等高,它们的体积之和是 36cm3,圆锥的体积是__________cm3。
一个圆锥的底面周长是18.84cm ,高是 3cm,它的体积是__________立方厘米。