如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图象与反比例函数y=(n-3)/x的图象相交于A,P两点.
(1)求m,n的值与A的坐标;
(2)求证:△CPD∼△AEO;
(3)求sin∠CDB的值.
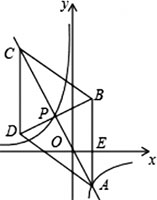
如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图象与反比例函数y=(n-3)/x的图象相交于A,P两点.
(1)求m,n的值与A的坐标;
(2)求证:△CPD∼△AEO;
(3)求sin∠CDB的值.

解答过程见word版
某蓄电池的电压为48V,使用此电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为I=48/R.当R=12Ω时,I的值为______A.
点(1,y1 ),(2,y2 ),(3,y3 ),(4,y4)在反比例函数y=4/x图像上,则y1,y2,y3,y4中最小的是【 】
如图,Rt△OAB与Rt△OBC位于平面直角坐标系中,∠AOB=∠BOC=30°,BA⊥OA,CB⊥OB,若AB=√3,反比例函数y=k/x(k≠0)恰好过点C,则k=________.
如图,在平面直角坐标素中,O(0,0),A(3,1),B(1,2),反比例函数y=k/x(k≠0)的图像过▱OABC的顶点C,则k=______.
如图,已知直角三角形ABC中AO=1,将△ABC绕O点旋转至△A'B'O的位置,且A'在OB中点,B'在反比例函数y=k/x上,则k的值为________.
如图,在同一平面直角坐标系中,直线y=k1x(k1≠0)与双曲线y=k2/x(k2≠0)相交于A,B两点,已知点A的坐标为(1,2),则点B的坐标为【 】