如图,Rt△OAB与Rt△OBC位于平面直角坐标系中,∠AOB=∠BOC=30°,BA⊥OA,CB⊥OB,若AB=√3,反比例函数y=k/x(k≠0)恰好过点C,则k=________.
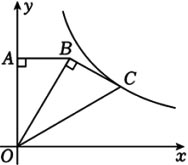
如图,Rt△OAB与Rt△OBC位于平面直角坐标系中,∠AOB=∠BOC=30°,BA⊥OA,CB⊥OB,若AB=√3,反比例函数y=k/x(k≠0)恰好过点C,则k=________.

4√3(解答过程见word版)
某蓄电池的电压为48V,使用此电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为I=48/R.当R=12Ω时,I的值为______A.
点(1,y1 ),(2,y2 ),(3,y3 ),(4,y4)在反比例函数y=4/x图像上,则y1,y2,y3,y4中最小的是【 】
根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(㎡)的反比例函数,其函数图象如图所示,当S=0.25㎡时,该物体承受的压强p的值为______Pa.
在平面直角坐标系xOy中,若点A(2,y1),B(5,y2)在反比例函数y=k/x(k>0)的图像上,则y1 _____ y2(填“>”“=”或“<”).
如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数y=1/x的图像经过点C,y=k/x(k≠0)的图像经过点B.若OC=AC,则k=________.
如图,双曲线y=k/x经过Rt△OBC斜边上的点A,且满足AO/AB=2/3,与BC交于点D,S△BOD=21,则k=________.
如图,已知点A在反比例函数y=k/x(x<0)上,作Rt△ABC,点D为斜边AC的中点,连接DB并延长交y轴于点E.若△BCE的面积为8,则k=________.
如图,已知∠AOX=30°,OA=2,AB⊥OA,AB=OA,则B的坐标为________.
如图,ΔABC中,点E在边AC上,EB=EA,∠A=2∠CBE,CD垂直于BE的延长线于点D,BD=8,AC=11,则边BC的长为_______.
如图, RT△ABC中∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6,则另一直角边BC的长为________.
在△ABC中,∠ABC=90°,若AC=100,sinA=3/5,则AB的长是【 】
已知△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D.若△ABC的一条边长为6,则点D到直线AB的距离为________.(结果要化简,不能含三角函数)
在ΔABC中,∠ABC=90°,AB=2,BC=3,点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为________.