如图,双曲线y=k/x经过Rt△OBC斜边上的点A,且满足AO/AB=2/3,与BC交于点D,S△BOD=21,则k=________.
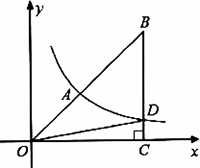
如图,双曲线y=k/x经过Rt△OBC斜边上的点A,且满足AO/AB=2/3,与BC交于点D,S△BOD=21,则k=________.

8过A作AE⊥x轴于点E,∵S△OAE=S△OCD∴SAECB=S△BOD=21,∵AE//BC,∴△OAE∼△OBC,∴S△OAE/S△OBC =(OA/OB)²=4/25,∴S△OAE=4,k=8...
查看完整答案如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数y=1/x的图像经过点C,y=k/x(k≠0)的图像经过点B.若OC=AC,则k=________.
如图所示,点P(3a,a)是反比例函数y=k/x(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为【 】
如图,双曲线y=k/x(k>0)与⊙O在第一象限内交于P、Q两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为________.
已知点A(a,y1),B(a+1,y2)在反比例函数y=(m2+1)/x (m是常数)的图像上,且y1<y2则a的取值范围是________.
如图,正比例函数y=kx与函数y=6/x的图像交于A,B两点,BC//x轴,AC//y轴,则S△ABC=________.
若反比例函数的图象经过点(1,-2),则该反比例函数的解析式(解析式也称表达式)为_________.
如图,已知反比例函数过A,B两点,A点坐标(2,3),直线AB经过原点,将线段AB绕点B顺时针旋转90°得到线段BC,则C点坐标为________.
在平面直角坐标系xOy中,矩形OABC的点A在函数y=1/x(x>0)的图像上,点C在函数y=-4/x(x<0)的图像上,若点B的横坐标为-7/2,则点A的坐标为【 】
如图, RT△ABC中∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6,则另一直角边BC的长为________.
在ΔABC中,∠ABC=90°,AB=2,BC=3,点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为________.
如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB. (1)若AE=1,求△ABD的周长;(2)若AD=1/3 BD,求tan∠ABC的值.
如图,边长为1的正方形ABCD中,点E为AD的中点,连接BE,将ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
如图,已知∠BAC=60°,AD是角平分线且AD=10,作AD的垂直平分线交AC于点F,作DE⊥AC,则△DEF的周长为____________.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB'C',使点C'落在AB边上,连结BB',则sin∠BB'C'的值为【 】
如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直一部分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为________.