如图,抛物线y=1/2 x2-3/2 x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行于BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π)
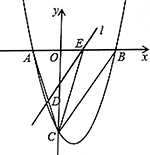
如图,抛物线y=1/2 x2-3/2 x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行于BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π)

(1)已知:抛物线y=1/2 x2-3/2 x-9;当x=0时,y=-9,则:C(0,-9);当y=0时,1/2 x2-3/2 x-9=0,得x_1=-3,x_2=6,则:A(-3,0),B(6,0);∴AB=9,OC=9.(2)∵ED//BC,∴△AED∽△ABC,∴S△AED/S△ABC =(AE/AB)2,即s/(1/2×9×9)=(m/9)2,得:s=1/2 m2 (0<m<9).(3)∵S△ACE=1/2 AE∙OC=1/2 m×9=9/2 m,∴S△CDE=S△ACE-S△ADE...
查看完整答案