如图,已知点A在反比例函数y=k/x(x<0)上,作Rt△ABC,点D为斜边AC的中点,连接DB并延长交y轴于点E.若△BCE的面积为8,则k=________.
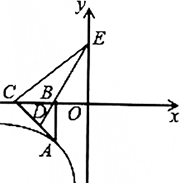
如图,已知点A在反比例函数y=k/x(x<0)上,作Rt△ABC,点D为斜边AC的中点,连接DB并延长交y轴于点E.若△BCE的面积为8,则k=________.

16∵△BCE的面积为8,∴1/2 BC⋅OE=8∴BC⋅OE=16,∵点D为斜边AC的中点,∴DB=DC,∴∠DBC=∠DCB=∠EBO,又∵∠EOB=∠ABC,∴△EOB∼△ABC,∴BC/OB=...
查看完整答案泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的【 】
已知ΔABC的周长为16,点D,E,F分别为ΔABC三条边的中点,则ΔDEF的周长为【 】
如图,BC//DE,且BC<DE,AD=BC=4,AB+DE=10,则AE/AC的值为__________.
如图,在ΔABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D,若BC=4,则CD的长为_________.
如图,每个小正方形边长均为1,则图中的三角形(阴影部分)与下图中△ABC相似的是【 】
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为【 】
在Rt△ABC中,∠C=90°,AD平分∠CAB,BE平分∠ABC,AD,BE相交于点F,且AF=4,EF=√2,则AC=________.
如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数y=1/x的图像经过点C,y=k/x(k≠0)的图像经过点B.若OC=AC,则k=________.
如图,双曲线y=k/x经过Rt△OBC斜边上的点A,且满足AO/AB=2/3,与BC交于点D,S△BOD=21,则k=________.
已知点A(x1,y1 ),B(x2,y2 ),C(x3,y3 )都在反比例函数y=k/x (k<0)的图像上,且x1<x2<0<x3,则y1,y2,y3的大小关系是【】
如图,点A是反比例函数y=3/x图象上任意一点,过点A分别作x轴,y轴的垂线,垂足为B,C,则四边形OBAC的面积为_______.
如图,一次函数y=kx-1的图象与反比例函数y=m/x的图象交于A、B两点,其中A点坐标为(2,1).(1)试确定k、m的值;(2)求B点的坐标.