如图是由小正方形组成的5×7网格,每个小正方形的顶点叫做格点.矩形ABCD的四个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
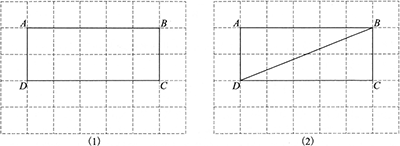
(1)在图(1)中,先在边AB上画点E,使AE=2BE,再过点E画直线EF,使EF平分矩形ABCD的面积;
(2)在图(2)中,先画△BCD的高CG,再在边AB上画点H,使BH=DH.
如图是由小正方形组成的5×7网格,每个小正方形的顶点叫做格点.矩形ABCD的四个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.

(1)在图(1)中,先在边AB上画点E,使AE=2BE,再过点E画直线EF,使EF平分矩形ABCD的面积;
(2)在图(2)中,先画△BCD的高CG,再在边AB上画点H,使BH=DH.
如图,在ΔABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D,若BC=4,则CD的长为_________.
如图,每个小正方形边长均为1,则图中的三角形(阴影部分)与下图中△ABC相似的是【 】
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为【 】
在Rt△ABC中,∠C=90°,AD平分∠CAB,BE平分∠ABC,AD,BE相交于点F,且AF=4,EF=√2,则AC=________.
泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的【 】
已知ΔABC的周长为16,点D,E,F分别为ΔABC三条边的中点,则ΔDEF的周长为【 】
如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF【 】
已知:如图,E、F在AC上,AD//CB且AD=CB,∠D=∠B.求证:AE=CF.
如图所示、△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.(1)求证:△AOC≌△BOD;(2)若AD=1,BD=2,求CD的长.
如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是【 】
如图,在四边形ABCD中,AD=BC,AC=BD,AC与BD相交于点E.求证:∠DAC=∠CBD.
如图是由 个小正方体组合成的几何体,该几何体的俯视图是【 】
下图是由一个长方体和一个圆锥组成的几何体,它的主视图是【 】
如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是【 】
下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是【 】
某正方体的每个面上都有一个汉字,如图是它的一种表面展开图,那么在原正方体中,与“伏”字所在面相对面上的汉字是【 】
下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是【 】
神奇的自然界处处蕴含着数学知识,动物学家在鹦鹉螺外壳上发现,其每圈螺纹的直径与相邻螺纹直径的比约为0.618.这体现了数学中的【 】