初中数学-中考试题(甘肃省天水市 2020年二次函数)

单项选择（2020年甘肃省天水市）

若函数y=ax²+bx+c(a≠0)的图象如图所示，则函数y=ax+b和y=c/x在同一平面直角坐标系中的图象大致是【】

A、

B、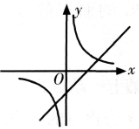

C、

D、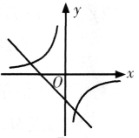

答案解析

B

讨论

初中数学

下列图形中，是中心对称图形但不是轴对称图形的是【】

如图所示，PA、PB分别与⊙O相切于、两点，点为⊙O上一点，连接AC、BC，若∠P=70°，则∠ACB的度数为【】

某小组8名学生的中考体育分数如下：39，42，44，40，42，43，40，42.该组数据的众数、中位数分别为【】

某正方体的每个面上都有一个汉字，如图是它的一种表面展开图，那么在原正方体中，与“伏”字所在面相对面上的汉字是【】

天水市某网店2020年父亲节这天的营业额为341000元，将数341000用科学记数法表示为【】

下列四个实数中，是负数的是【】

如图，抛物线y=x2-x-3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．直线l与抛物线交于A，D两点，与y轴交于点E，点D的坐标为(4,-3)．（1）请直接写出A，B两点的坐标及直线l的函数表达式；（2）若点P是抛物线上的点，点P的横坐标为 (m≥0)，过点P作PM⊥x轴，垂足为M．PM与直线l交于点N，当点N是线段PM的三等分点时，求点P的坐标；（3）若点Q是y轴上的点，且∠ADQ=45°，求点Q的坐标．

问题情境：如图①，点E为正方形ABCD内一点，∠AEB=90°，将RtΔABE绕点B按顺时针方向旋转90°，得到ΔCBE'（点A的对应点为点C），延长AE交CE'于点F，连接DE．猜想证明：（1）试判断四边形BE' FE的形状，并说明理由；（2）如图②，若DA=DE，请猜想线段CF与FE'的数量关系并加以证明；解决问题：（3）如图①，若AB=15，CF=3，请直接写出DE的长．

图①是某车站的一组智能通道闸机，当行人通过时智能闸机会自动识别行人身份，识别成功后，两侧的圆弧翼闸会收回到两侧闸机箱内，这时行人即可通过．图②是两圆弧翼展开时的截面图，扇形ABC和DEF是闸机的“圆弧翼”，两圆弧翼成轴对称，BC和EF均垂直于地面，扇形的圆心角∠ABC=∠DEF=28°，半径BA=ED=60cm，点A与点D在同一水平线上，且它们之间的距离为10cm．（1）求闸机通道的宽度，即BC与EF之间的距离（参考数据：sin⁡28°≈0.47，cos⁡28°≈0.88，tan⁡28°≈0.53）；（2）经实践调查，一个智能闸机的平均检票速度是一个人工检票口平均检票速度的2倍，180人的团队通过一个智能闸机口比通过一个人工检票口可节约3分钟，求一个智能闸机平均每分钟检票通过的人数．

阅读与思考下面是小宇同学的数学日记，请仔细阅读并完成相应的任务．×年×月×日星期日没有直角尺也能作出直角今天，我在书店一本书上看到下面材料：木工师傅有一块如图①所示的四边形木板，他已经在木板上画出一条裁割线AB，现根据木板的情况，要过AB上的一点C，作出AB的垂线，用锯子进行裁割，然而手头没有直角尺，怎么办呢？办法一：如图①，可利用一把有刻度的直尺在AB上量出CD=30cm，然后分别以D，C为圆心，以50cm与40cm为半径画圆弧，两弧相交于点E，作直线CE，则∠DCE必为90°．办法二：如图②，可以取一根笔直的木棒，用铅笔在木棒上点出M，N两点，然后把木棒斜放在木板上，使点M与点C重合，用铅笔在木板上将点N对应的位置标记为点Q，保持点N不动，将木棒绕点N旋转，使点M落在AB上，在木板上将点M对应的位置标记为点R．然后将RQ延长，在延长线上截取线段QS=MN，得到点S，作直线SC，则∠RCS=90°．我有如下思考：以上两种办法依据的是什么数学原理呢？我还有什么办法不用直角尺也能作出垂线呢？……任务：（1）填空；“办法一”依据的一个数学定理是_____________________________________；（2）根据“办法二”的操作过程，证明∠RCS=90°；（3）①尺规作图：请在图③的木板上，过点C作出AB的垂线（在木板上保留作图痕迹，不写作法）；②说明你的作法依据的数学定理或基本事实（写出一个即可）

二次函数

如图1，关于x的二次函数y=-x²+bx+c经过点A(-3,0),C(0,3)，点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上.(1)求抛物线的解析式；(2) DE上是否存在点P到AD的距离与到x轴的距离相等？若存在求出点P，若不存在请说明理由；(3)如图2，DE的左侧抛物线上是否存在点F，使2S△FBC=3S△EBC？若存在求出点F的坐标,若不存在请说明理由.

如图，抛物线y=ax²+2x-3与x轴交于A,B两点，且B(1,0).(1)求抛物线的解析式和点A的坐标；(2)如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；(3)如图2，已知直线y=2/3 x-4/9分别与x轴、y轴交于C,F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE.问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由.

如图，抛物线y=ax²+bx+2经过点A(-1,0),B(4,0)，交y轴于点C.(1)求抛物线的解析式（用一般式表示）；(2)点D为y轴右侧抛物线上一点，是否存在点D使S△ABC=2/3 S△ABD？若存在请直接给出点D的坐标；若不存在请说明理由；(3)将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长.

二次函数y=ax²+bx+c(a≠0)的图像如图所示，下列结论正确提【】

已知顶点为A的抛物线y=a(x-1/2)²-2经过点B(-3/2,2)，点C(5/2,2).(1)求抛物线的解析式；(2)如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠0PM=∠MAF，求△POE的面积；(3)如图2，点Q是折线A-B-C上一点，过点Q作QN//y 轴，过点E作EN//x轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN1，若点N1落在x轴上，请直接写出Q点的坐标.

已知y=ax²+bx+c(a≠0)的图像如图，则y=ax+b和y=c/x的图像为【】

竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=-5t2+v0t+h0表示，其中h0 (m)是物体抛出时离地面的高度，v0 (m/s)是物体抛出时的速度．某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出，小球达到的离地面的最大高度为【】

已知抛物线 y=x2-(m+1)x+2m+3.(1) 当m=0时，请判断点(2,4)是否在该抛物线上；(2) 该抛物线的顶点随着m的变化而移动，当顶点移动到最高处时，求该抛物线的顶点坐标；(3) 已知点E(-1,-1),F(3,7)，若该抛物线与线段EF只有一个交点，求该抛物线顶点横坐标的取值范围.

已知抛物线y=1/2 x2+x+c与x轴没有交点.(1)求c的取值范围;(2)试确定直线y=cx+1经过的象限，并说明理由.

如图,抛物线y=1/2 x2-3/2 x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行于BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π)

坐标系与函数

如图，已知点A在反比例函数y=k/x(x<0)上，作Rt△ABC，点D为斜边AC的中点，连接DB并延长交y轴于点E.若△BCE的面积为8，则k=________.

假设小丽的眼睛距地面1.5米，当她站在C点时，测出旗杆A的仰角为 30°，如果向前走 10米到达点E，此时的仰角为60°，求旗杆AB的高度.

某兴趣小组借助无人飞机航拍校园如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°.已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度.(结果保留根号)

如图，学校环保社成员想测量斜坡 CD 旁一棵树AB 的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知斜坡CD的长度为20m，DE的长为10cm，则树AB的高度是【】m.

如图，一次函数y=kx+b 与反比例函数y=m/x(x>0)交于A(2,4),B(a,1)，与x轴，y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=m/x(x>0)的表达式；(2)求证：AD=BC.

如图，A,B是函数y=12/x上两点，P为一动点，作PY//y轴，PA//x轴，下列说法正确的是【】①△AOP≅△BOP；②S△AOP=S△BOP；③若OA=OB，则OP平分∠AOB；④若S△BOP=4，则S△ABP=16.

如图，在Rt△ABC中，∠ABC=90°,C(0,-3),CD=3AD，点A在反比例函数y=k/x图像上，且y轴平分∠ACB.求k=________.

已知点A(x1,y1 )，B(x2,y2 )，C(x3,y3 )都在反比例函数y=k/x (k<0)的图像上，且x1<x2<0<x3，则y1，y2，y3的大小关系是【】

已知反比例函数解析式y=k/x的图象经过(1，-2)，则k=________.

如图,直线y=2x-6与反比例函数y=k/x(x>0)的图像交于点A(4,2),与x轴交于点B.(1)求k的值及点B的坐标; (2)在ⅹ轴上是否存在点C,使得AC=AB？若存在,求出点C的坐标;若不存在,请说明理由.