如图,一次函数y=kx+b 与反比例函数y=m/x(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=m/x(x>0)的表达式;
(2)求证:AD=BC.
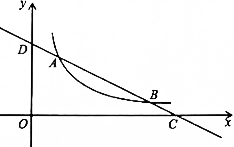
如图,一次函数y=kx+b 与反比例函数y=m/x(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=m/x(x>0)的表达式;
(2)求证:AD=BC.

(1)将点A(2,4)代入y=m/x中,得m=8,∴反比例函数的解析式为y=8/x,将点B(a,1)代入y=8/x中,得a=8,∴B(8,1),将A(2,4),B(8,1)代入y=kx+b中,得,解得,∴一次函数的解析式为y=-1/2 x+5.(2)∵直线AB...
查看完整答案如图,一次函数y=kx-1的图象与反比例函数y=m/x的图象交于A、B两点,其中A点坐标为(2,1).(1)试确定k、m的值;(2)求B点的坐标.
已知反比例函数解析式y=k/x的图象经过(1,-2),则k=________.
如图所示,点P(3a,a)是反比例函数y=k/x(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为【 】
如图,双曲线y=k/x(k>0)与⊙O在第一象限内交于P、Q两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为________.
已知点A(a,y1),B(a+1,y2)在反比例函数y=(m2+1)/x (m是常数)的图像上,且y1<y2则a的取值范围是________.