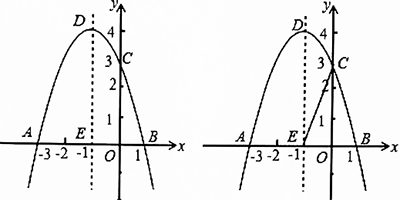
如图1,关于x的二次函数y=-x²+bx+c经过点A(-3,0),C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.
(1)求抛物线的解析式;
(2) DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;
(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.
如图1,关于x的二次函数y=-x²+bx+c经过点A(-3,0),C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.
(1)求抛物线的解析式;
(2) DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;
(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.

(1)∵二次函数经过点A(-3,0),C(0,3),∵,解得b=-2,c=3,∴抛物线的解析式为y=-x²-2x+3.(2)存在.当P在∠DAB的平分线上时,如图1,作PM⊥AD,设P(-1,m),则PM=PD∙sin∠ADE=(4-m)∙√5/5,PE=m,∵PM=PE,∴(4-m)∙√5/5=m,解得m=√5-1,∴P(-1,√5-1);当P在∠DAB的外角平分线上时,如图2,作PN⊥AD,设P(-1,n),则PN=PD∙sin∠ADE=(4-n)∙√5/5,PE=-n,∵PN=PE,∴(4-n)∙√5/5=-n,解得n=-√5-1,∴P(-1,-√5-1);综上可知,存在满足条件的P点,其坐标为(-1,√5-1),(-1,-√5-1).(3)∵抛物线的解析式...
查看完整答案抛物线y=ax2+bx+c经过点(-1,0),(3,0),且与y轴交于点(0,-5),则当x=2时,y的值为【 】
在平面直角坐标系xOy中,点M(-4,2)关于x轴对称的点的坐标是【 】
在平面直角坐标系xOy中,若抛物线y=x2+2x+k与x轴只有一个交点,则k=________.
如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是【 】
已知二次函数y=ax2+bx+c的图像开口向下,对称轴为直线x=-1,且经过点(-3,0),则下列结论正确的是【 】
某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对(m,n),在坐标系中进行描点,则正确的是【 】