某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对(m,n),在坐标系中进行描点,则正确的是【 】
A、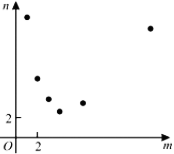
B、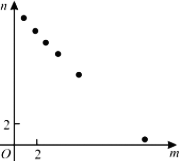
C、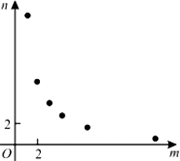
D、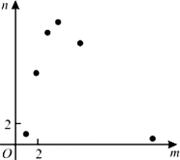
某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对(m,n),在坐标系中进行描点,则正确的是【 】
A、
B、
C、
D、
C
【解析】
依题意,mn=12,符合反比例函数.
在平面直角坐标系xOy中,矩形OABC的点A在函数y=1/x(x>0)的图像上,点C在函数y=-4/x(x<0)的图像上,若点B的横坐标为-7/2,则点A的坐标为【 】
若点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=8/x的图像上,则x1,x2,x3的大小关系是【 】
如图,点A是反比例函数y=3/x图象上任意一点,过点A分别作x轴,y轴的垂线,垂足为B,C,则四边形OBAC的面积为_______.
如图,一次函数y=kx-1的图象与反比例函数y=m/x的图象交于A、B两点,其中A点坐标为(2,1).(1)试确定k、m的值;(2)求B点的坐标.
如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是【 】
如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是【 】
已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为【 】
已知点P(a+1,2a-3)关于x轴的对称点在第一象限,则a的取值范围是【 】
在平面直角坐标系xOy中,点M(-4,2)关于x轴对称的点的坐标是【 】
如图所示,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为_________.
如图,在平面直角坐标系中,ΔOAB的顶点A,B的坐标分别为(3,),(4,0).把ΔOAB沿x轴向右平移得到ΔCDE,如果点D的坐标为(6,),则点E的坐标为_________.