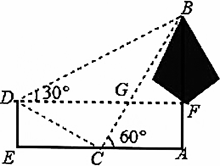
如图,学校环保社成员想测量斜坡 CD 旁一棵树AB 的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是【 】m.
A、20√3
B、30
C、30√3
D、40
如图,学校环保社成员想测量斜坡 CD 旁一棵树AB 的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是【 】m.

A、20√3
B、30
C、30√3
D、40
B在Rt△CDE中,CD=20,DE=10m,∴sin∠DCE=10/20=1/2,∴∠DCE=30°,∵∠ACB=60°,DF//AE,∴∠BGF=60°,∴∠ABC=30°,∠DCB=90°.∵∠...
查看完整答案