如图,抛物线y=ax²+2x-3与x轴交于A,B两点,且B(1,0).
(1)求抛物线的解析式和点A的坐标;
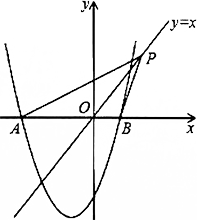
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y=2/3 x-4/9分别与x轴、y轴交于C,F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.

如图,抛物线y=ax²+2x-3与x轴交于A,B两点,且B(1,0).
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y=2/3 x-4/9分别与x轴、y轴交于C,F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.


(1)把B(1,0)代入y=ax²+2x-3,得a+2-3=0,解得a=1,∴抛物线的解析式为y=x²+2x-3.令y=0,则x²+2x-3=0,解得x=1或x=-3,∴A点的坐标为(-3,0);(2)若y=x平分∠APB,则∠APO=∠BPO,如图,若P点在x轴上方,PA与y轴交点于B',由于点P在直线y=x上,可知∠POB=∠POB'=45°,在△BPO和△B'PO中,,∴△BPO≅△B'PO(ASA),∴OB=OB'=1,设直线AP的解析式为y=kx+b,把A,B'两点坐标代入得:,解得,∴直线AP的解析式为y=1/3 x+1,联立,解得,∴P点的坐标为(3/2,3/2).若P点在x轴下方,同理可得△BPO≅△B'PO,∴∠APO=∠BPO=∠B'PO,与∠B'PO在∠APO内部矛盾,即此时没有满足条件的P点,综上可知P点的坐标为(3/2,3/2).(3)作QH⊥CF于点H,由CF为y=2/3 x-4/9,...
查看完整答案某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对(m,n),在坐标系中进行描点,则正确的是【 】
如图,点A(0,3)、B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是【 】
已知函数y=,则自变量x的取值范围是___________.
如图所示,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为_________.
如图,在平面直角坐标系中,ΔOAB的顶点A,B的坐标分别为(3,),(4,0).把ΔOAB沿x轴向右平移得到ΔCDE,如果点D的坐标为(6,),则点E的坐标为_________.