初中数学-中考试题(广东省深圳市 2016年一元一次不等式组)

计算题（2016年广东省深圳市）

解不等式组：.

答案解析

解不等式①得x<2，

解不等式②得x≥-1，

所以，原不等式组的解集是：-1≤x<2.

讨论

初中数学

计算：|-2|-2cos60°+(1/6)-1-(π-√3)0.

如图,四边形ABCO是平行四边形，AO=2,AB=6，点C在x轴的负半轴上，将ABCO绕点A逆时针旋转得到ADEF,AD经过点O，点F恰好落在x轴的正半轴上，若点D在反比例函数y=k/x的图像上，则k的值为________.

如图，在▱ABCD中，AB=3,BC=5，以点B为圆心，以任意长为半径作弧，分别交BA,BC于点P,Q，再分别以P,Q为圆心，以大于1/2 PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为__________.

已知一组数据x1,x2,x3,x4的平均数是5，则数据x1+3,x2+3,x3+3,x4+3的平均数是________.

分解因式：a²b+2ab²+b³=__________.

如图，CB=CA,∠ACB=90°，点D在边BC上(与B,C不重合)，四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB:S四边形CBFG=1:2；③∠ABC=∠ABF；④AD²=FQ⋅AC.其中正确的结论的个数是【】

如图，在扇形AOB中∠AOB=90°，正方形CDEF的顶点C是弧(AB) ̂的中点，点D在OB上,点E在OB 的延长线上，当正方形CDEF的边长为2√2时,阴影部分的面积为【】

给出一种运算：对于函数y=xn,规定y'=nxn-1.例如：若函数y=x4则有y'=4x3.已知函数y=x3，则方程y'=12的解是【】

施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原计划多 50 米，才能按时完成任务，求原计划每天施工多少米。设原计划每天施工x米，则根据题意所列方程正确的是【】

下列命题正确的是【】

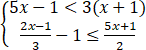不等式(组)

甲工厂将生产的Ⅰ号、Ⅱ号两种产品共打包成5个不同的包裹，编号分别为A、B、C、D、E，每个包裹的重量及包裹中Ⅰ号、Ⅱ号产品的重量如下：包裹编号 Ⅰ号产品重量/吨 Ⅱ号产品重量/吨包裹的重量/吨A 5 1 6B 3 2 5C 2 3 5D 4 3 7E 3 5 8甲工厂准备用一辆载重不超过19.5吨的货车将部分包裹一次运送到乙工厂.(1)如果装运的I号产品不少于9吨，且不多于11吨，写出一中满足条件的装运方案______(写出要装运包裹的编号);(2)如果装运的1号产品不少于9吨，且不多于11吨，同时装运的II号产品最多，写出满足条件的装运方案______(写出要装运包裹的编号).

解不等式组，请按下列步骤完成解答.(1)解不等式①,得__________；(2)解不等式②,得__________；(3)把不等式①和②的解集在数轴上表示出来； (4)原不等式组的解集是______________.

若2x+y=1，且0<y<1.则x的取值范围为__________.

解不等式1+2(x-1)≤3，并在数轴上表示解集.

不等式3x-1>5的解集是【】

已知a,b是两个连续整数a<√3-1<b则a,b分别是【】

广东省一元一次不等式组

北京市一元一次不等式组

四川省成都市一元一次不等式组

解不等式组请结合题意填空，完成本题的解答.（Ⅰ）解不等式①，得____________；（Ⅱ）解不等式②，得____________；（Ⅲ）把不等式①和②的解集在数轴上表示出来：（Ⅳ）原不等式的解集为________________.

一元一次不等式组

山东省青岛市一元一次不等式组

不等式组的解集是【】

海南省一元一次不等式组

北京市一元一次不等式组

不等式组的解集是【】

解不等式组：并把它的解集在数轴上表示出来.

不等式组的解集为【】

江苏省盐城市一元一次不等式组

解不等式组并求它的所有整数解的和．

某学校组织340名师生进行长途考察活动，带有行李170件，计划租用甲、乙两种型号的汽车10辆.经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李.(1)请你帮助学校设计所有可行的租车方案；(2)如果甲车的租金为每辆2000元，乙车的租金为每辆1800元，问哪种可行方案使租车费用最省？